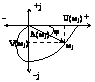Ответы на экзаменационные вопросы (теория информации, линейные системы), страница 34

Частотная передаточная функция при каждом значении частоты ω является комплексной величиной и может быть представлена в показательном виде:

 ,где

,

Годограф функции , т.е. геометрическое место концов векторов  при изменении угловой частоты от 0 до ¥, представляет собой АФЧХ.

ЛАЧХ: при построении ее по оси абсцисс откладывается частота в логарифмическом масштабе (lgw). По оси ординат ЛАЧХ откладывается в равномерном масштабе логарифмическая амплитуда L=20lgА дБ. L – амплитуда А, выраженная в децибелах.

ЛФЧХ: ось абсцисс такая же, как и у ЛАЧХ, а по оси ординат в равномерном масштабе откладывают фазу y в угловых градусах или радианах.

ЛЧХ удобны тем, что небольшим графиком может быть охвачен широкий диапазон, при этом одинаково наглядно изменение частотных свойств как на малых , так на средних и высоких частотах.

В ряде случаев можно пренебречь кривизной ЛАЧХ на некоторых небольших участках частоты и заменить их с большой точночтью прямыми – асимптотами. Тогда ЛАЧХ называется асимптотической и ее расчет заметно облегчается.

31. Рекуррентные алгоритмы моделирования линейных систем автоматического управления.

Передаточная функция К(z) эквивалентной импульсной системы является z – преобразование от импульсной переходной характеристики h(t) приведённой непрерывной части

                 (1)

Для линейных систем с постоянными сосредоточенными параметрами дискретные передаточные функции эквивалентных импульсных систем даётся в виде дробно-рациональной функции:

                  (2)

которая приводит к рекурентному алгоритму

             (3)

Метод z – преобразований.

Входной сигнал V(t), действующий на линейную систему с передаточной функцией К(s), при  достаточно малом шаге дискретизации заменяется модулированной последовательностью d - функции с огибающей Dt V[n] и периодом Dt. Это соответствует выбору в качестве интерполирующего фильтра безинерционного усилителя с коэффициентом усиления к=Dt, т.е.

                             (4)

При таком виде интерполяции импульсная переходная характеристика приведённой непрерывной части с точностью до множителя Dt  совпадает с импульсной переходной характеристикой непрерывной системы. Следовательно дискретная переходной характеристикой непрерывной системы. Следовательно дискретная переходная функция К_*(z), эквивалентной импульсной системы равны z – преобразованию дискретной импульсной переходной характеристики непрерывной системы, умноженной на Dt.

                    (5)

Импульсная переходная характеристика непрерывной системы с передаточной функцией:

           (6)

Имеем в общем случае d+1 различных полюсов s_u , u=1¸d (корни уравнения К₂(s)=0) кратности r_u каждый, так что V₁+…+V₂ = m, согласно теоремы разложения представляется в виде:

                              (7)

где             (8)

Из (7) следует:                    (9)                   где q_u = s_uDt