Механика \ Телемеханика

Ответы на экзаменационные вопросы (теория информации, линейные системы), страница 37

                           Q – невязка параметров.

                   - система нормальных уравнений

                 т – операция транспонирования

                    FтF – квадратная матрица.

FтF=Ф – матрица Фишера, обратная матрица от Ф – математическая точность.

         Эта вся процедура называется МНК (метод наименьших квадратов), позволяет найти неизвестные коэффициенты.

(Dуi)2 – регрессия, появляющаяся в результате эксперимента данных.

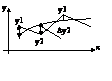В МНК проводят линию, которая проходит между точками у1, у2,…..уn. Используя МНК кривую регрессии можно точно построить.

Метод наименьших квадратов. (МНК)

Для стационарных объектов и нестационарных объектов по способу обработки результатов идентификации.

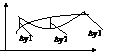Используемый метод наименьших квадратов (МНК) позволяет решать линейные системы.

у¹f(x)            

 - процедура МНК, Х – матрица плана.

Предпосылки для использования МНК:

-  входная величина измеряется точно, а выходная с большой погрешностью;

-  погрешности измерения распределены по нормальному (гаусовскому) закону распределения;

-  независимость результатов измерения.

ОМНК – обобщенный метод наименьших квадратов.

Метод планирования эксперимента.

Разработали: Фишер и Стьюдент.              - матрица Фишера.

Регрессионный анализ (МНК - составная часть метода)

-с помощью метода Стьюдента можно определить .

Дисперсионный анализ позволяет стоить линейные модели, но для качественных факторов.

 - нелинейная модель относительно неизвестных факторов.

Цель использования МНК:- наименьшие затраты; получить более точные измерения.

Рекуррентный МНК позволяет уйти от обратной матрицы, т.к. она трудно вычисляется на ЭВМ.

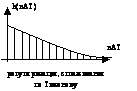Некорректные задачи. Регуляризация – сглаживание.

 - похоже на МНК.

a - параметр регуляризации, который подбирается таким образом, чтобы было сглаживание.

Подставляя разложение (9) в (5) и используя свойства линейности z – преобразования получим:

              (10)

Передаточную функцию Кum(z) (z-преобразование от nm equn ) можно найти по таблицам дискретного преобразования Лапласа или же, поскольку  то, на основании теоремы дифференцирования z – преобразования по параметру можно записать:

Выражение для Кum(z) первых производных приведены в таблице 1.

Скачать файл