2. ![]()
![]() Опред. оценку степени нелинейного преобразования n ® n.
Опред. оценку степени нелинейного преобразования n ® n.
3. Определить время переходного процесса.
4. Опред. полосу пропускания.
5. Определить статические характеристики.
Описывается
дробно-рациональной передаточной функцией: ![]() ;
p > m
;
p > m
6. Необходимо определить степени полинома числителя и знаменателя (p и m).
7. Определить имеются ли в системе степень затухания.
Задача непараметрической идентификации.
Определить частотные характеристики: нормирование имп. переходная характеристика, нормирование относительно статических характеристик.
![]() ,
значение аi,
,
значение аi, ![]()
Эти характеристики связаны между собой преобразованием Фурье.
Необходимо определить значение
аi, ![]() .
.
37. Теорема квантования по времени (теорема Котельникова).
Согласно теореме В.А. Котельникова, функция, имеющая ограниченный спектр, полностью определяется своими дискретными значениями в точках, расположенных на расстоянии 2П/2wмдруг относительно друга, где wм– максимальная круговая частота в спектре функции; т.е. любая непрерывная функция, спектр которой ограничен частотой Fmax может быть полностью восстановлена по её дискретным значениям, взятым через интервалы времени Dt£1/(2Fmax) (по теореме В.А. Котельникова можно определить шаг квантования).
Однако имеется ряд затруднений для практического применения этой теоремы, связанных с тем, что все сообщения передаваемые в телемеханике, ограничены во времени.
Практически теорему Котельникова можно применять с поправкой: Dt = 1 / (h2Fmax)
где h - коэффициент, зависящий от точности воспроизведения функции и способа интерполяции;
при линейной интерполяции ![]()
при ступенчатой - hст = (3¸5) hл
d - относительная погрешность в %
Восстановить квантованную по времени функцию на приёмной стороне можно с помощью ступенчатой или линейной интерполяции либо методом Котельникова.
Чаще всего применяют ступенчатую интерполяцию и наиболее редко – фильтрацию по Котельникову.
При восстановлении, квантованной функции по Котельникову нужно знать все дискретные точки как предыдущие так и последующие, или, во всяком случае для практической реализации должно быть известно несколько точек до и после интервала, в котором происходит интерполяция.
Значение последующих точек возможно лишь в системах, допускающих запаздывание в передаче информации.
Иногда восстановление функции, квантованной во времени, с шагом подсчитанным по теореме Котельникова, производят с помощью фильтра нижних частот, который выделяет постоянную и низкочастотные составляющие спектру передаваемой функции.
Задача параметрической идентификации.
1. Определяем значения постоянной времени.
2. Определяем коэффициенты
![]() аi ,
аi , ![]() .
.
Задача ускоренной параметрической идентификации.
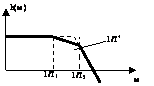 Имеется частотная характеристика
системы третьего порядка
Имеется частотная характеристика
системы третьего порядка
Для того чтобы решить эти задачи необходимо составить задачи идентификации.
Имеется объект, описывается в виде функционалов:
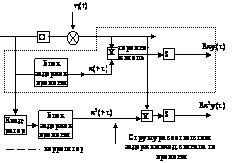 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.