Оптимізація просторово-часових параметрів функціонування системи керування, що навчається

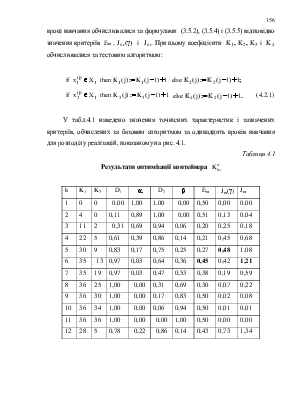
РОЗДІЛ 4

 ОПТИМІЗАЦІЯ просторово-часових ПАРАМЕТРІВ ФУНКЦІОНУВАННЯ СК, ЩО НАВЧАєТЬСЯ

Відомі на початку розвитку теорії розпізнавання образів спроби побудови в процесі навчання "точних" контейнерів класів розпізнавання, що обумовлюють отримання потенційної (близької до одиниці) достовірності розпізнавання, виявилися неспроможними через такі принципові обставини:

·  перетин класів розпізнавання, який має місце в практичних задачах контролю та керування;

·  обмежений на практиці обсяг навчальної вибірки, що ускладнює перевірку основної статистичної гіпотези через неповну апріорну інформацію про властивості та ймовірнісні характеристики слабо формалізованого процесу;

·  висока обчислювальна трудомісткість алгоритмів побудови "точних" контейнерів.

У МФСВ концепція побудови в рамках геометричного підходу алгоритмів навчання займає проміжне положення між алгоритмами побудови "точних" контейнерів і непараметричними алгоритмами ітераційної оптимізації апроксимуючих роздільних функцій, дозволяючи цим виключити недоліки і зберегти переваги цих алгоритмів. Реалізація ітераційної процедури (2.3.8) оптимізації просторово-часових параметрів навчання, потребує як вибору структури параметрів функціонування СК, так і ретельного дослідження їх впливу на функціональну ефективність навчання системи. Залежно від призначення та специфіки функціонування СК, що навчаються, такими параметрами можуть бути:

·   геометричні параметри контейнерів : еталонні вектори  , вершини яких є геометричними центрами відповідних контейнерів, і радіуси  {d_m}  контейнерів, які визначаються в кодовій відстані Хеммінга як  , де  ;

·  система полів контрольних допусків на ознаки розпізнавання  ;

·   рівні селекції  двійкових координат еталонних векторів;

·  крок квантування в часі  t   вхідних реалізацій образу;

·  параметри словника ознак розпізнавання;

·  параметри нормалізації зображень;

·  параметри впливу зовнішнього середовища на образи;

·  параметри плану навчання та інші.

Процедура ітераційної оптимізації параметрів навчання за МФСВ спрямована на побудову в радіальному базисі оптимальних контейнерів класів розпізнавання, які забезпечують максимальну асимптотичну достовірність класифікатора, що характеризується функціональною ефективністю навчання СК розпізнавати образи. У цьому розділі розглядаються приклади реалізації алгоритмів оптимізації основних просторово-часових параметрів функціонування СК і досліджується їх вплив на функціональну ефективність навчання системи.

4.1. Базовий алгоритм навчання

Призначенням базового алгоритму навчання  LEARNING  є обчислення інформаційного КФЕ навчання СК, пошук глобального максимуму функції критерію в робочій області її визначення й оптимізація геометричних параметрів контейнерів, яка реалізується операторами контуру оптимізації (2.4.2) згідно з діаграмою (2.4.1) відображення множин, що застосовуються в процесі навчання. Вхідною інформацією для навчання за базовим алгоритмом у загальному випадку є дійсний масив реалізацій образу ; система полів контрольних допусків    на ознаки розпізнавання і рівні селекції    координат війкових еталонних векторів-реалізацій образу, які за умовчанням дорівнюють  0,5  для всіх класів розпізнавання.

Розглянемо етапи реалізації базового алгоритму навчання LEARNING:

1.  Формування бінарної навчальної матриці 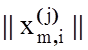 , елементи якої

визначаються за правилом:

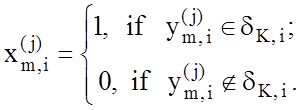                                                                         (4.1.1)

2. Формування масиву еталонних двійкових векторів-реалізацій  , елементи якого визначаються за правилом:

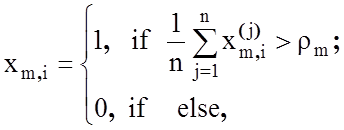                                                                   (4.1.2)

де  r_m - рівень селекції координат вектору  .

3. Розбиття множини еталонних векторів на пари найближчих ²сусідів²: =<x_m , x_с >, де  x_с - еталонний вектор сусіднього класу ,за таким алгоритмом:

а) структурується множина еталонних векторів, починаючи з вектора  x₁  базового класу  , який характеризує найбільшу функціональну ефективність СК;

б) формується матриця кодових відстаней між еталонними векторами розмірності  M ´ M;

в) для кожної строки матриці кодових відстаней знаходиться мінімальний елемент, який належить стовпчику вектора - найближчого до вектора, що визначає строку. При наявності декількох однакових мінімальних елементів вибирається з них будь-який, оскільки вони є рівноправними;

г) формується структурована множина елементів попарного розбиття  , яка задає план навчання.

4. Оптимізація кодової відстані  d_m  відбувається за процедурою (2.3.5). При цьому приймається  .

5.Процедура закінчується при знаходженні глобального максимуму КФЕ в робочій області визначення його функції: 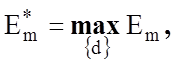 де  - множина радіусів концентрованих гіперсфер, центр яких визначається вершиною  .

Таким чином,  базовий  алгоритм навчання є частковим випадком  алгоритмів навчання (2.3.8) і (2.3.9):

                                                      .                                         (4.1.3)