Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 4

Рис..4.3. Залежність КФЕ від радіуса контейнера 

Аналіз значень точнісних характеристик на кожному кроці навчання, який збільшує радіус контейнера    дозволяє знайти як саму робочу область визначення критерію  , так і екстремальні значення першої та другої достовірностей:   і   На рис. 4.3 показано , що в робочій області критерій набуває свого максимуму 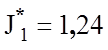  при оптимальному значенні радіуса контейнера  , яке дорівнює  . При цьому забезпечується як максимальне значення КФЕ, так і максимальна повна достовірність розпізнавання реалізацій класу  , яка дорівнює  .

4.3 Алгоритми екзамену

Алгоритми екзамену за МФСВ можуть мати різну структуру залежно від розподілу реалізацій образу, що розпізнаються. Обов’язковою умовою їх реалізації є забезпечення однакових структурованості і параметрів формування як для навчальної, так і для екзаменаційної матриць.

За наявності чіткого розбиття, яке було утворено на етапі навчання, алгоритм екзамену за МФСВ має такі вхідні дані:

·  M - кількість класів, які нечіткий регулятор навчен розпізнавати;

·   - масив еталонних двійкових векторів-реалізацій образу, які визначають центри відповідних оптимальних контейнерів класів розпізнавання, побудованих на етапі навчання;

·  {} - масив оптимальних радіусів побудованих на етапі навчання відповідних контейнерів;

·   - масив двійкових векторів-реалізацій образу, що розпізнається;

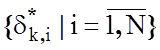·   - оптимальна СКД на ознаки розпізнавання, яку визначено на етапі навчання.

За умовчанням приймається рівень селекції  r_m= 0,5.

Розглянемо кроки реалізації агоритма екзамену при застосуванні гіпотези чіткої компактності реалізацій образу:

1. Формування лічильника класів розпізнавання: .

2. Формування лічильника числа реалізацій, що розпізнаються: .   

3. Порівняння: якщо  , то виконується крок 4, інакше - крок 5.

4. Формування лічильника    позитивних результатів порівняння.

5. Порівняння: якщо  j  n , то виконується крок 2, інакше – крок 6.   

6. Порівняння: якщо  k >j / 2, то виконується крок 8, інакще – крок 7.

7. Порівняння: якщо m  M, то виконується крок 1, інакше  – крок 8.

8. Визначення класу  , до якого належить екзаменаційна матриця.

Якщо в процесі екзамену порівняння на кроці 6 не дало позитивного результату, то може бути запущено алгоритм факторного класифікаційного аналізу, з метою донавчання системи, або алгоритм прогностичної класифікації, з метою підтвердження необхідності перенавчання СК. 

Для нечіткого розбиття алгоритм екзамену за МФСВ ґрунтується на аналізі значень функції належності, яка має вигляд (2.3.10) і обчислюється для кожної реалізації, що розпізнається. Розглянемо кроки реалізації алгоритму екзамену при нечіткому розбитті:

1. Формування лічильника    класів розпізнавання.    

2. Формування лічильника числа реалізацій, що розпізнаються: .

3. Обчислення кодової відстані  .

4. Обчислення функції належності за виразом (2.3.10):

                                 

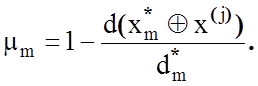
5. Порівняння: якщо  j  n , то виконується крок 2, інакще – крок 6.

6. Порівняння: якщо  m  M, то виконується крок 1, інакще – крок 7.     

7. Визначення класу  , до якого належить екзаменаційна реалізація, наприклад, за умови 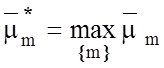 , де 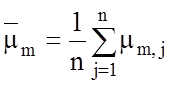 - усереднене значення функцій належності для реалізацій класу  , або видача повідомлення: «Клас не визначено»,  якщо 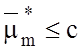 . Тут с- порогове значення.

Опис структурних схем алгоритмів екзамену для чіткого та нечіткого розбиття наведено в додатку  В.

Таким чином, алгоритми екзамену за МФСВ відрізняються незначною обчислювальною трудомісткістю, що дозволяє їх реалізовувати у реальному темпі часу. Що стосується вибору чіткого або нечіткого алгоритмів екзамену, то у загальному випадку при розв’язанні задач кластер-аналізу перевагу необхідно надавати нечіткому алгоритму екзамену, оскільки у процесі донавчання системи апріорна кількість параметрів навчання, що оптимізуються, може бути недостатньою для побудови безпомилкового вирішального правила. При     прийнятті рішень за апріорно класифікованими навчальними матрицями (навчання з “учителем”) доцільно реалізовувати чіткий алгоритм екзамену. Але і в цьому випадку нечіткий алгоритм є працездатним, оскільки він розглядається по відношенню до чіткого алгоритму як загальний.