|
Ρ1 |
E1 |
D1 |
β |
d1 |
d |
dc |
|
0,40 |
0,674989 |
0,80 |
0,00 |
39 |
12 |
55 |
|
0,42 |
0,710603 |
0,84 |
0,00 |
33 |
14 |
4 |
|
0,44 |
0,710603 |
0,84 |
0,00 |
33 |
14 |
38 |
|
0,46 |
0,710603 |
0,84 |
0,00 |
31 |
14 |
38 |
|
0,48 |
0,701025 |
0,83 |
0,00 |
30 |
14 |
43 |
|
0,50 |
0,754381 |
1,00 |
0,12 |
38 |
12 |
45 |
|
0,52 |
0,794417 |
1,00 |
0,09 |
37 |
12 |
48 |
|
0,54 |
0,809527 |
1,00 |
0,08 |
35 |
12 |
48 |
|
0,56 |
0,809527 |
1,00 |
0,08 |
35 |
12 |
51 |
|
0,58 |
0,765397 |
0,99 |
0,08 |
33 |
12 |
53 |
|
0,60 |
0,794417 |
1,00 |
0,09 |
33 |
12 |
51 |
На даному прикладі вивчимо
вплив рівня селекції на центрування контейнера ![]() . Оскільки навчальна матриця для
кожного класу складалася тільки із 100 реалізацій, а координати еталонних
векторів класів
. Оскільки навчальна матриця для
кожного класу складалася тільки із 100 реалізацій, а координати еталонних
векторів класів ![]() і
і ![]() обчислювалися як вибіркові середні
відповідних навчальних вибірок, то геометричний центр контейнера
обчислювалися як вибіркові середні
відповідних навчальних вибірок, то геометричний центр контейнера ![]() не збігається з центром
розсіювання реалізацій класу
не збігається з центром
розсіювання реалізацій класу ![]() . На рис. 4.11 показано розподіл у
радіальному базисі частот проекцій реалізацій класів
. На рис. 4.11 показано розподіл у
радіальному базисі частот проекцій реалізацій класів ![]() (темні дискрети) і
(темні дискрети) і ![]() (світлі дискрети) на вісь, що
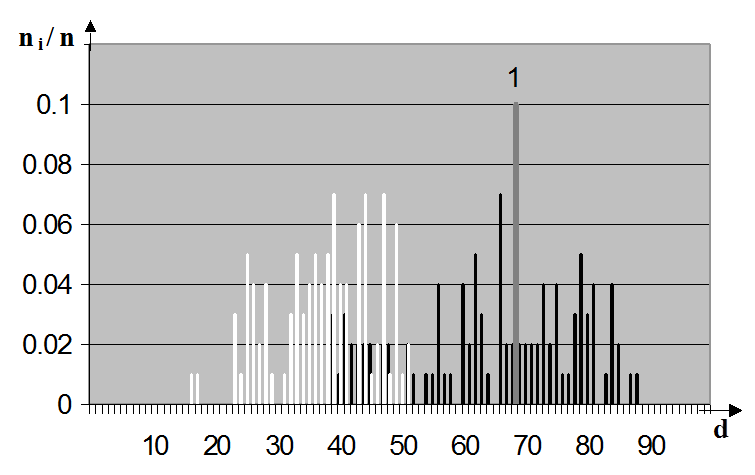
проходить через центри цих класів. Тут мітка “1” позначає положення вершини вектора
х1 при r1 = 0,50 (рис.4.11а) і положення вершини цього вектора при оптимальному
рівні селекції
(світлі дискрети) на вісь, що
проходить через центри цих класів. Тут мітка “1” позначає положення вершини вектора
х1 при r1 = 0,50 (рис.4.11а) і положення вершини цього вектора при оптимальному
рівні селекції ![]() (рис.4.11б). Оцінюючи візуально зміщення емпіричного центру
розсіювання в процесі оптимізації ріня селекції можна стверджувати, що при
оптимальному рівні селекції геометричний центр контейнера
(рис.4.11б). Оцінюючи візуально зміщення емпіричного центру
розсіювання в процесі оптимізації ріня селекції можна стверджувати, що при
оптимальному рівні селекції геометричний центр контейнера ![]() , який
визначається вершиною двійкового еталонного вектора-реалізації, одержаного при
статистичному усередненні реалізацій образу за умови мінімального обсягу
навчальної вибірки, є більш наближеним до теоретичного центра розсіювання
реалізацій класу
, який
визначається вершиною двійкового еталонного вектора-реалізації, одержаного при
статистичному усередненні реалізацій образу за умови мінімального обсягу
навчальної вибірки, є більш наближеним до теоретичного центра розсіювання
реалізацій класу ![]() у порівнянні з початковим (неоптимальним) рівнем селекції,
який дорівнював за умовчанням r1 = 0,50.
у порівнянні з початковим (неоптимальним) рівнем селекції,
який дорівнював за умовчанням r1 = 0,50.
Аналіз табл. 4.4 показує, що при
оптимальному рівні селекції ![]() відбулося збільшення міжцентрової кодової відстані,
яка стала дорівнювати
відбулося збільшення міжцентрової кодової відстані,
яка стала дорівнювати ![]() (
(![]() при r=0,50). Оскільки при цьому одночасно відбулося зменшення
радіуса оптимального контейнера (
при r=0,50). Оскільки при цьому одночасно відбулося зменшення
радіуса оптимального контейнера (![]() ) у порівнянні із вихідним
) у порівнянні із вихідним ![]() при r=0,50), то можна зробити висновок, що
оптимізація рівня селекції за алгоритмом (4.7.2) призводить як до максимізації
міжцентрової кодової відстані, так і до мінімізації середньої відстані між
реалізаціями класу
при r=0,50), то можна зробити висновок, що
оптимізація рівня селекції за алгоритмом (4.7.2) призводить як до максимізації
міжцентрової кодової відстані, так і до мінімізації середньої відстані між
реалізаціями класу ![]() , а це, в свою чергу, призводить до зменшення відносного коефіціента
нечіткої компактності реалізацій образу (2.2.2), який характеризує ступінь
перетину класів розпізнавання.
, а це, в свою чергу, призводить до зменшення відносного коефіціента
нечіткої компактності реалізацій образу (2.2.2), який характеризує ступінь
перетину класів розпізнавання.
ї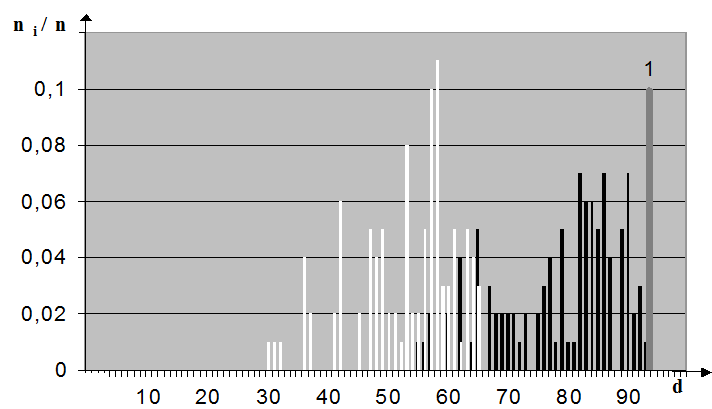
a)
б)
Рис. 4.11. Частота розподілу реалізацій класів ![]() і
і ![]() :
:
а) r1 = 0,50; б) r1 = 0,56.
Таким чином, центрування контейнерів класів розпізнавання шляхом оптимізації рівнів селекції координат війкових векторів призводить до зменшення ступеню перетину класів розпізнавання, що у відповідності з формулою (3.8.6) збільшує асимптотичну повну достовірність класифікатора та відповідає як дистанційно-максимальному, так і дистанційно-мінімальному принципам теорії розпізнавання образів [63,67,68].
4.8. Оптимізація кроку квантування в часі реалізацій образу
У рамках МФСВ розглянемо оптимізацію (в інформаційному розумінні) такого важливого параметра функціонування СК, що навчається, як крок квантування в часі реалізацій образу на вході нечіткого регулятора. Задачу оптимізації кроку квантування t розглянемо як часткову задачу інформаційного синтезу СК, що навчається.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.