Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 11

Розглянемо схему реалізації паралельного алгоритму оптимізації нормованих допусків за критерієм (4.6.2).

1.  Обчислюється еталонна реалізація дискрет   шляхом статистичного усереднення значень дискрет реалізацій  {}  класу    і задається стартове значення параметра  .

2.   Формується масив 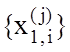   двійкових векторів-реалізацій класу   за правилом:

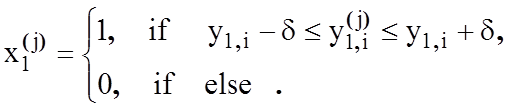                                            (4.6.3)

3.  Будується для двійкових векторів-реалізацій класу    матриця  кодових відстаней  , елементи якої визначаються за правилом:

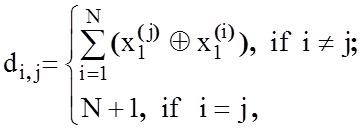                                                                 (4.6.4)

де  i, j – змінні строк і стовпців матриці    відповідно. Таким чином, нульовим діагональним елементам матриці    штучно присвоюється значення   – максимальна кодова відстань у матриці.

4. Формуються пари найближчих сусідніх реалізацій 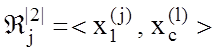  за умови, що  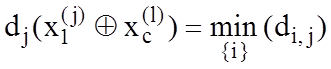, де  – найближча до вектора   реалізація, отримана на  l-му кроці оптимізації.

5. Обчислюється за формулою (4.6.2) вибіркова середня відстань    для розбиття  .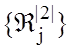

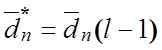6. Порівнюється поточне середнє значення  (l)  з попереднім  (l-1). Якщо  , то    і виконується крок 1, інакше    і  

7 Формується оптимальна СНД  , де нижні допуски дорівнюють   і верхні допуски - .

З метою ілюстрації роботи наведеного вище алгоритму, розглянемо визначення оптимальної за критерієм (4.6.2) системи нормованих допусків на ознаки в задачі розпізнавання спектрограм, отриманих на масспектрометрі    МІ-12-01 АТ виробництва ВАТ “Selmi” (Суми, Україна). На рис. 4.7 наведено дві реалізації-спектрограми класу  . Тут на вісі абсцис відкладено довжину хвилі в нанометрах, а на вісі ординат – значення струму електронного підсилювача в мікроамперах. Якщо поява дискрет, значення яких перевершують шумовий поріг, у реалізаціях відбувається детерміновано, тобто при однакових для даного хімічного елементу значеннях довжини хвилі, то їх амплітуди, як видно з рис. 4.7, мають випадкові значення.

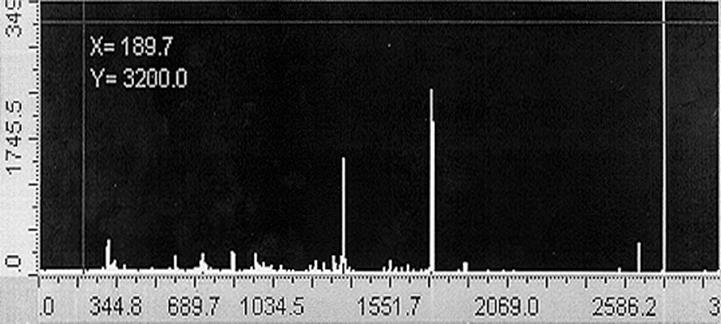                                                  а)

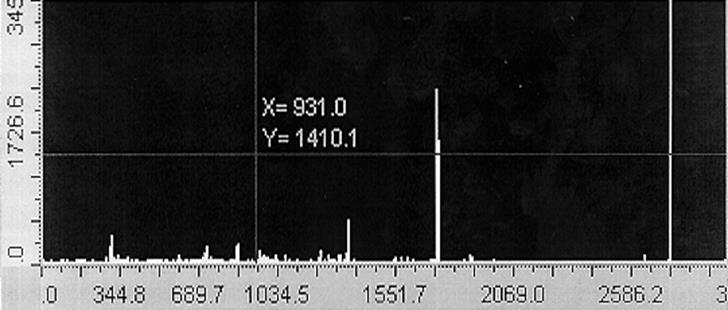
                                                    б)

Рис. 4.7. Реалізації спектрограм класу 

У табл. 4.2 наведено для прикладу сім двійкових реалізацій класу  , сформованих за правилом (2.6.3) при  . Кожна з цих реалізацій містить 12 ознак, які приймають одиничне значення, якщо їх дискрети перебільшують шумовий поріг.

Таблиця 4.2

Двійкові реалізації спектрограм класу   (d=40)

№ реалі- зації	Координати  векторів
	1	2	3	4	5	6	7	8	9	10	11	12
1	1	1	1	1	0	1	0	1	0	1	0	0
2	1	1	1	1	1	1	0	0	0	1	0	0
3	1	1	1	0	1	1	0	1	1	1	0	0
4	0	1	1	1	1	1	0	0	1	1	0	1
5	1	1	1	1	1	1	1	1	0	1	0	0
6	1	1	0	0	1	1	0	1	0	1	1	0
7	1	1	0	1	1	1	0	1	0	1	0	0

На базі табл. 4.2 сформовано за правилом (4.6.4) матрицю кодових відстаней, яку наведено в табл. 4.3.

Таблиця 4.3

Матриця кодових відстаней