Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 15

Нехай для двох класів розпізнавання   і    відома навчальна матриця 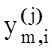 ||||, . Дано структурований вектор параметрів функціонування  , де   - радіус контейнера  , поле контрольних допусків на ознаки розпізнавання і крок квантування в часі реалізацій образу відповідно. Для наочності нехай рівні селекції за умовчанням дорівнюють  . Тоді в тестовому алгоритмі навчання (2.3.8) структурований алгоритм оптимізації кроку квантування вхідних реалізацій має вигляд:

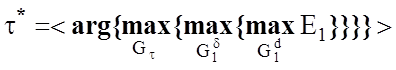                             ,                              (4.8.1)

де      область допустимих значень кроку квантування в часі реалізацій образу, яка визначається за теоремою Шеннона-Котєльнікова  .

          В алгоритмі (4.8.1) зовнішній цикл реалізується послідовністю операторів контуру (2.4.8) оптимізації кроку квантування  t  у діаграмі (2.4.5).

Розглянемо схему реалізації такого алгоритму:

1.  Обнуління лічильника кроків квантування: t:=0.

2.  Запуск лічильника кроків квантування: t:=t+1.

3.  Реалізується один із алгоритмів оптимізації СКД на ознаки      розпізнавання (послідовний LEARNING–1, паралельний LEARNING–2  або послідовно-паралельний).

4.  Якщо в робочій області визначення інформаційного критерію  , то виконується пункт 2, інакше пункт 5.

5.  ;   і  “ЗУПИН”.

Реалізацію алгоритму (4.8.1) розглянемо на прикладі побудови оптимального контейнера для базового класу  , який забезпечує максимальну інформаційну міру різноманітності між класом    і поточним класом    у процесі автофокусування растрового електронного мікроскопа РЕМ-103 за зображенням зразка, що досліджується. Початкове розфокусоване зображення (клас ) і поточне зображенняа (клас  ) наведено відповідно на рис.4.9а і рис.4.9б. Для формування бінарних навчальних матриць яскравості для зображень    і    оптимальне контрольне симетричне поле допусків для всіх ознак розпізнавання (N=150), які мають однакову шкалу виміру [0;255] в градаціях яскравості чорно-білого графічного редактора, визначалося за паралельним алгоритмом оптимізації і складало  |d_{К, і} | = 24 градації яскравості (). На рис. 4.12 наведено графіки залежності ентропійного інформаційного критерію (3.5.2) від радіуса контейнера    при різних кроках квантування в часі реалізацій образу. Графік на рис. 4.12а отримано для кроку квантування  t, який дорівнює одному пікселю. Відповідно подано графіки на рис. 4.12б  для  t=2, на  рис. 4.12в  для  t=3,  на рис. 4.12г для  t=4, на рис. 4.12д для  t=5  і на     рис. 4.12е  для  t=6пікселів. На рис. 4.12 робочі області визначення функції критерію виділено подвійною штриховкою.

Аналіз графіків, наведених на рис.4.12, показує, що максимальному значенню критерію    відповідає оптимальне значення кроку квантування реалізацій образу, яке дорівнює  t^*=2.

а)	б)
в) д)	г)  е)

Рис. 4.12. Залежність КФЕ навчання від радіуса контейнера класу  :

а) t=1; б) t=2; в) t=3; г) t=4; д) t=5; е) t=6

У табл. 4.5 подано для розглянутих кроків квантування значення критерію  , оптимальних радіусів    контейнерів для класу    і екстремальні значення відповідних точнісних характеристик при двохальтернативному рішенні.

Таблиця 4.5

Експериментальні дані оптимізації кроку дискретизації реалізацій образу

t
1	0,60	85	0,76	0,24	0,99	0,01
2	0,61	44	0,80	0,20	0,99	0,01
3	0,58	28	0,76	0,24	0,99	0,01
4	0,51	19	0,61	0,39	0,99	0,01
5	0,52	14	0,58	0,42	0,99	0,01
6	0,50	13	0,73	0,27	0,97	0,03