![]() – структурований вектор ознак розпізнавання;
– структурований вектор ознак розпізнавання;
![]() – структурований вектор стартових параметрів
контрольних допусків на ознаки розпізнавання;
– структурований вектор стартових параметрів
контрольних допусків на ознаки розпізнавання;
![]() – кількість прогонів ітераційної процедури
послідовної оптимізації контрольних допусків;
– кількість прогонів ітераційної процедури
послідовної оптимізації контрольних допусків;
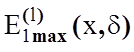 – максимальне значення КФЕ в робочій
області його визначення при l-му прогоні
ітераційної процедури;
– максимальне значення КФЕ в робочій
області його визначення при l-му прогоні
ітераційної процедури;
![]() – найбільший глобальний максимум функції
КФЕ в області її значень;
– найбільший глобальний максимум функції
КФЕ в області її значень;
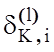 – значення параметра поля контрольних допусків
для і-ої ознаки, яке отримано при l-му
прогоні ітераційної процедури та дорівнює половині інтервалу
– значення параметра поля контрольних допусків
для і-ої ознаки, яке отримано при l-му
прогоні ітераційної процедури та дорівнює половині інтервалу 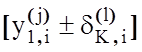 ;
;
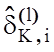 – екстремальне значення параметра поля
контрольних допусків для і-ї ознаки;
– екстремальне значення параметра поля
контрольних допусків для і-ї ознаки;
![]() – оптимальне значення поля контрольних
допусків для і-ї ознаки:
– оптимальне значення поля контрольних
допусків для і-ї ознаки:
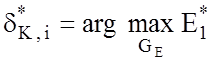 .
.
З урахуванням (2.3.8) і введених позначень структурований алгоритм послідовної оптимізації поля контрольних допусків на ознаки розпізнавання приймає вигляд:
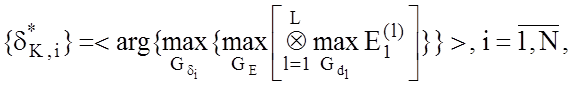 (4.4.1)
(4.4.1)
де ![]() – області допустимих
значень поля контрольних допусків
– області допустимих
значень поля контрольних допусків
для і-ої ознаки, критерію оптимізації і кодової
відстані ![]() відповідно;
відповідно;
![]() – символ операції повторення.
– символ операції повторення.
Розглянемо
послідовність ![]() , де
, де
![]()
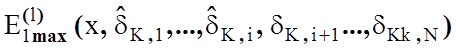 –
–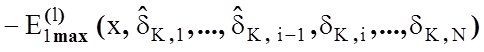 .
.
Т в е р д ж е
н н я 4.4.1. Послідовність ![]() монотонно спадає і обмежена знизу.
монотонно спадає і обмежена знизу.
Д о в е д е н н я. Покажемо, що ![]() . Це
легко доводиться за індукцією. Нехай при
. Це
легко доводиться за індукцією. Нехай при ![]() для
першої ознаки знайдено екстремальне значення
для
першої ознаки знайдено екстремальне значення 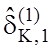 за
умови, що значення контрольних допусків для інших ознак залишаються стартовими.
Тоді має місце:
за
умови, що значення контрольних допусків для інших ознак залишаються стартовими.
Тоді має місце:
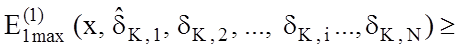
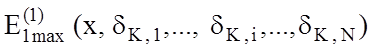 .
.
Оскільки за властивістю інформаційного критерію 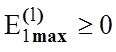 , то відношення рівності може бути тільки
за умови, що стартове значення
, то відношення рівності може бути тільки
за умови, що стартове значення ![]() дорівнює
екстремальному. Так само справедливо і для всіх Nекстремальних значень
дорівнює
екстремальному. Так само справедливо і для всіх Nекстремальних значень 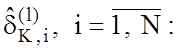
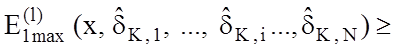
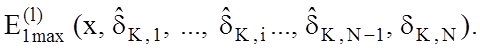
Таким чином, послідовність ![]() є спадною і обмеженою знизу, оскільки її
члени додатні. Але не ясно, чи є послідовність стаціонарною, тобто чи існує
таке
є спадною і обмеженою знизу, оскільки її
члени додатні. Але не ясно, чи є послідовність стаціонарною, тобто чи існує
таке ![]() , що для будь-якого l >L має місце
, що для будь-якого l >L має місце![]() . Відповідь на це запитання дає
така теорема.
. Відповідь на це запитання дає
така теорема.
Т е о р е м а 4.4.1. Ітераційний алгоритм послідовної оптимізації контрольних допусків на ознаки розпізнавання (4.4.1) збігається з імовірністю одиниця.
Д о в е д е н н я. Для
доведення теореми необхідно та достатньо показати, що екстремальні поля
контрольних допусків 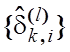 збігаються відповідно до
оптимальних
збігаються відповідно до
оптимальних ![]() Припустимо, що послідовність
Припустимо, що послідовність ![]() , яка за твердженням спадна і
обмежена знизу, збігається на L-му прогоні ітераційної процедури і вона є стаціонарною,
тобто
, яка за твердженням спадна і
обмежена знизу, збігається на L-му прогоні ітераційної процедури і вона є стаціонарною,
тобто ![]() . Тоді маємо:
. Тоді маємо: 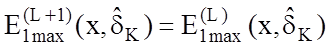 . Але
звідси не обов’язково витікає, що
. Але
звідси не обов’язково витікає, що 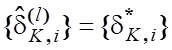 , оскільки функція
, оскільки функція ![]() не є взаємно-однозначною. Покажемо
концептуально, що все-таки існує
не є взаємно-однозначною. Покажемо
концептуально, що все-таки існує 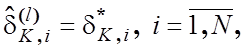 для будь-якого
для будь-якого ![]() . У силу дистанційно-максимального принципу
розпізнавання образів, у процесі оптимізації розбиття
. У силу дистанційно-максимального принципу
розпізнавання образів, у процесі оптимізації розбиття ![]() для
найближчих сусідніх класів
для
найближчих сусідніх класів ![]() і
і ![]() повинна виконуватися умова:
повинна виконуватися умова: 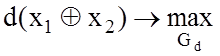 з обмеженнями (2.3.4) і (2.3.6). Нехай
існує для функції
з обмеженнями (2.3.4) і (2.3.6). Нехай
існує для функції 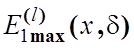 множина екстремальних
параметрів:
множина екстремальних
параметрів: 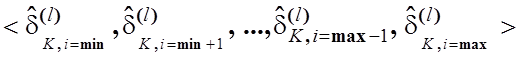 . Оскільки збільшення параметра
. Оскільки збільшення параметра 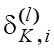 збільшує ймовірність
переходу і-ї координати еталонного вектора-реалізації
збільшує ймовірність
переходу і-ї координати еталонного вектора-реалізації ![]() в одиницю, то за умови, що еталонний
вектор
в одиницю, то за умови, що еталонний
вектор ![]() є одиничним, має місце:
є одиничним, має місце:
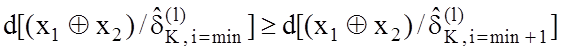 .
.
Таким чином, можна
стверджувати, що припущення про стаціонарність послідовності ![]() є справедливим, оскільки в
силу максимально-дистанційного принципу розпізнавання образів за умови
є справедливим, оскільки в
силу максимально-дистанційного принципу розпізнавання образів за умови 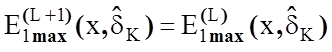 існує оптимальне значення параметру поля
контрольних допусків
існує оптимальне значення параметру поля
контрольних допусків 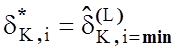 .
.
Так само, виходячи із концепції запропонованого методу автоматичної класифікації – МФСВ, доведемо збіжність паралельного алгоритму оптимізації контрольних допусків на ознаки розпізнавання. Для цього введемо такі позначення:
l – змінна
кроків збільшення параметра поля допусків ![]() ;
;
![]() – змінна поля допусків на ознаки
розпізнавання, область визначення якого
– змінна поля допусків на ознаки
розпізнавання, область визначення якого ![]() , де {Gi} – допустимі області значень
контрольних допусків для ознак розпізнавання;
, де {Gi} – допустимі області значень
контрольних допусків для ознак розпізнавання;
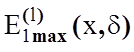 – значення КФЕ в робочій області його
визначення після l-го кроку зміни параметра
– значення КФЕ в робочій області його
визначення після l-го кроку зміни параметра ![]() ;
;
![]() – точне значення глобального максимуму КФЕ
навчання системи розпізнавати реалізації класу
– точне значення глобального максимуму КФЕ
навчання системи розпізнавати реалізації класу ![]() в
робочій області визначення його функції;
в
робочій області визначення його функції;
![]() – поле контрольних допусків, яке отримано після l-го кроку зміни параметра
– поле контрольних допусків, яке отримано після l-го кроку зміни параметра ![]() і дорівнює для
і-ї ознаки інтервалу
і дорівнює для
і-ї ознаки інтервалу 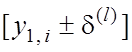 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.