Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 16

Оскільки інформаційна міра є мірою різноманітності двох об’єктів, то побудований на етапі навчання оптимальний контейнер класу    повинен на екзамені забезпечувати правильну класифікацію як реалізацій "свого", так і "чужого" класів. Тому як асимптотичну достовірність класифікаційного рішення, яке приймається на екзамені, слід розглядати повну ймовірність правильного прийняття рішень  , де  p₁, p₂ –апріорні (безумовні) ймовірності належності реалізацій зображень відповідним класам    і  . Відповідно асимптотична повна ймовірність помилкового прийняття рішень дорівнює . Оскільки апріорні ймовірності, як правило, невідомі, то за принципом  Бернуллі-Лапласа  приймемо гіпотези  рівноймовірними , тобто  p₁= p₂= 0,5, що моделює більш "важкі" статистичні умови прийняття рішень, але є виправданим у задачах пошуку екстремальних значень параметрів оптимізації. На рис. 4.13 наведено залежність асимптотичної повної ймовірності прийняття на екзамені помилкових рішень     від величини кроку квантування  t.

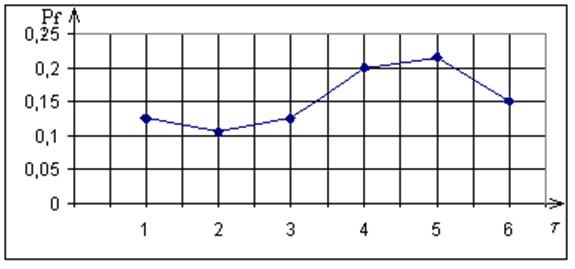
Рис. 4.13. Залежність асимптотичної повної ймовірності помилкових

рішень від кроку квантування

Аналіз рис. 4.13 підтверджує, що мінімальна асимптотична повна ймовірність помилкових рішень класифікатора за МФСВ дійсно має місце саме при

t = 2, яке і слід приймати за оптимальне значення. При цьому крок дискретизації, обчислений за теоремою Шеннона-Котєльнікова, може розглядатися як граничне значення оптимального у інформаційному розумінні кроку квантування в часі реалізацій образу. 

4.9. Особливості оптимізації контейнерів класів розпізнавання в   

радіальному базисі

При оптимізації контейнерів класів розпізнавання в радіальному базисі виникає необхідність їх центрування на кожному кроці навчання. Це пов’язано з тим, що центр контейнера задається вершиною еталонного вектора, координати якого визначаються як вибіркове середнє значень відповідних навчальних вибірок. Оскільки геометричний центр контейнера в практичних задачах не збігається з теоретичним центром розсіювання реалізацій образу, то це призводить до зменшення повної достовірності розпізнавання на екзамені. Розглянемо особливості обчислення інформаційного КФЕ і вплив  параметрів функціонування на ефективність навчання СК в рамках МФСВ при використанні репрезентативних навчальних вибірок малого обсягу.

Оптимізація контейнерів класів розпізнавання в рамках МФСВ зводиться до розв’язання задачі багатопараметричної оптимізації шляхом пошуку глобального максимуму інформаційного КФЕ навчання СК за багатоциклічною структурованою процедурою (2.3.8). При цьому проблема обчислення інформаційного критерію оптимізації контейнерів класів розпізнавання методологічно обумовлена способом урахування реалізацій образу в радіальному базисі.

У вище наведених прикладах реалізації алгоритмів оптимізації відповідних параметрів навчання обчислення модифікацій інформаційних КФЕ (3.5.2) і (3.5.5) на кожному кроці навчання здійснювалося шляхом оцінки відповідних точнісних характеристик:   і , де – кількість реалізацій класу  , які знаходяться або не знаходяться у контейнері    відповідно; – кількість реалізацій класу  , які знаходяться або не знаходяться у контейнері    відповідно; – кількість реалізацій одного класу. При цьому коефіцієнти і  обчислювалися за алгоритмом  (4.2.1).

Аналіз результатів фізичного моделювання показав, що використання алгоритму (4.2.1) для обчислення інформаційного КФЕ навчання призводить до зміщення центру розсіювання реалізацій образу відносно центру контейнера. Це обумовлює методологічну помилку, пов’язану із способом врахування реалізацій образу в радіальному базисі. Так, при реалізації  алгоритму (4.2.1) не враховується дійсне положення реалізацій образу відносно центру контейнера, а припускається, що всі реалізації образів знаходяться між вершинами еталонних векторів    і  , які є відповідно центрами контейнерів класів   і  , що не відповідає загальній гіпотезі компактності реалізацій образу. З метою усунення цього недоліку розглянемо модифікацію алгоритму обчислення інформаційного КФЕ, яка визначає положення кожної реалізації як відносно центрів класів, так і відносно вершини нульового вектора   у просторі ознак розпізнавання. Нехай  , де  ,  – кодові відстані  векторів   і    від вектора   у бінарному  просторі ознак відповідно. Тоді тестовий алгоритм обчислення коефіцієнтів  і  такий: