Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 9

Т в е р д ж е н н я  4.5.2.  Для того, щоб    було допустимим, необхідно і достатньо, щоб  М.

Дійсно, якщо М, то за лемою 4.5.2 М, тобто виконуються всі умови твердження  4.5.1.

Сформулюємо тепер умови допустимості перетворення шкал у термінах, пов’язаних безпосередньо зі шкалами. Для цього довжину всякої шкали    запишемо у вигляді  , де    взаємно просте з числами  2  і  5 ( - довільний індекс).

Т е о р е м а 4.5.1. Перетворення шкали  на шкалу  допустимо тоді, коли    ділить  .

Д о в е д е н н я. За твердженням 4.5.2, умова теореми виконується тоді і тільки тоді, коли коефіцієнт 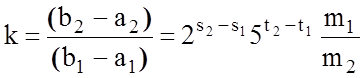   належить  М. Згідно з лемою 4.5.1 для цього необхідно та достатньо, щоб дріб    у запису, що нескорочений, мав у знаменнику тільки множники  2  і  5. Але за визначенням    є взаємно простим із цими числами. Таким чином, після скорочення дріб    є цілим числом, тобто    ділить  .

Н а с л і д о к  1. Найменша довжина шкали  , для якої існує допустиме перетворення на фіксовану шкалу    дорівнює одиниці. При  цьому   N₀.

Дійcно, найменше значення числа  ,  яке ділить    дорівнює одиниці, а найменше значення  для    і    дорівнює  нулю.

Н а с л і д о к 2. Найменша довжина шкали  , на яку існує допустиме перетворення фіксованої шкали    дорівнює . При цьому  N₀ .

Дійсно, найменше значення числа  , яке ділиться на  , дорівнює  . Найменші значення    дорівнюють  нулю.

Розглянемо питання, пов’язані з побудовою зведеного поля сімейства шкал.

Т е о р е м а  4.5.2.  Для того, щоб перетворення шкали  на кожну шкалу заданого сімейства , були допустимими, необхідно та достатньо, щоб    ділило  НСД, де НСД - найбільший спільний дільник. Найменша довжина такої шкали    дорівнює одиниці.

Д о в е д е н н я.  За теоремою 4.5.1 умова даної теореми виконується тоді і тільки тоді, коли    ділить  кожне  , тобто    ділить їх найбільший спільний дільник. Минимальне значення такого    дорівнює одиниці.

Т е о р е м а  4.5.3. Для того, щоб перетворення кожної шкали , заданого сімейства на шкалу  було допустимим, необхідно та достатньо, щоб НСК, де  НСК - найменше спільне кратне, ділило . Найменша можлива довжина такої шкали  дорівнює  НСК.

Дійсно, за теоремою 4.4.1 умова даної теореми рівносильна тому, що    кожне    ділить  . Але це виконується тоді і тільки тоді, коли НСК  ділить  .

Найменше можливе    дорівнює  НСК.

Назовемо шкали    і    еквівалентними, якщо обидва перетворення (4.5.1) и (4.5.2) є допустимими. Тоді із теореми 4.5.1 витікає така теорема.

Т е о р е м а 4.5.4. Шкала    еквівалентна шкалі    тоді і тільки тоді, коли  .

Н а с л і д о к 1. Найменша довжина шкали, яка еквівалентна заданій шкалі  , дорівнює  .

Із теореми 4.5.4 витікає так само, що відношення еквівалентності шкал рефлексивно, симетрично і транзитивно.

Для ілюстраціі застосування отриманих результатів розглянемо приклад визначення зведеного поля для трьох полів допусків, які будемо вважати шкалами довжиною 10, 12, и 20 відносних одиниць (градацій), тобто 

За теоремою 4.5.3 найменша можлива довжина зведеного поля допусків дорівнює   НСК(10; 12; 20).

Тепер перевіримо допустимість оберненого перетворення зведеного поля допусків на кожну задану шкалу. Для цього знайдемо НСД, і впевнимося, що дроб  /НСД(10,12, 20)  є цілим числом, тобто    ділить НСД і, таким чином, умови теореми 4.5.2  виконуються. Аналогічно можна показати, що сімейство шкал, наприклад, з довжиною   не має зведеного поля допусків, оскільки обернене перетворення його на кожну шкалу заданого сімейства є недопустимим у наведеному вище розумінні.

На підставі допускової концепції автоматизованого контролю і управління практичний інтерес становлять не стільки номінальні значення вхідних змінних, що відображають вхідну змінну на конституйовану функцію відгуку, скільки допустимі інтервали їх варіювання з метою забезпечення необхідної ефективності функціонування СК. Аналітичний розв’язок такої задачі в загальному вигляді відсутній. У рамках МФСВ вирішення цієї проблеми принципово можливо шляхом визначення інформаційної спроможності СК в процесі її алгоритмічного навчання. У МФСВ процес оптимізації контрольних допусків на ознаки розпізнавання за зведеним полем допусків у загальному випадку складається з таких етапів: