Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 5

4.4. Оптимізація контрольних допусків на ознаки розпізнавання

Оскільки контрольні допуски на значення ознак розпізнавання прямо впливають на геометричні параметри контейнерів класів розпізнавання, а отже і на асимптотичні точнісні характеристики нечіткого регулятора, то питання вибору СКД набуває важливого значення при розробці інформаційного забезпечення СК, що навчається. Якщо задача визначення системи нормованих (експлуатаційних) допусків на значення ознак знайшла хоча би свій розв’язок в рамках параметричного підходу математичної статистики [245], то аналітичне розв’язання задачі вибору СКД на ознаки, дослідження її впливу на функціональну ефективність СК і достовірність результатів розпізнавання все ще неодержано. Основними причинами такого стану є:

·  відсутність методів оптимізації параметрів функціонування складних систем за прямим та об’єктивним КФЕ;

·  статистична нестійкість, неоднорідність і обмеженість навчальної вибірки, що не дозволяє використовувати відомі методи параметричного підходу.

·  виправдане з метрологічної точки зору допущення про нормальність розподілу ймовірностей значень ознак розпізнавання при машинному прийнятті рішень призводить до збільшення помилки другого роду, оскільки контрольне поле допусків у цьому випадку береться завищеним.

Розглянемо підхід до оптимізації СКД на ознаки розпізнавання в рамках МФСВ. На рис. 4.4 показано симетричне (двобічне) поле допусків на значення  і-ї ознаки  .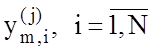

                    

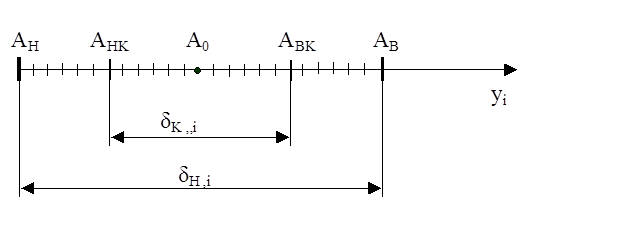
Рис. 4.4. Симетричне поле допусків на значення ознаки розпізнавання

На рис. 4.4 прийнято такі позначення: А₀ -номінальне значення ознаки  y_i; А_Н,  А_В - нижній і верхній нормовані допуски відповідно;  А_НК , А_ВК - нижній і верхній контрольні допуски відповідно; d_Н,і - нормоване поле допусків; d_К,і– контрольне поле допусків.

Існує декілька можливих стратегій зміни поля допусків  d_К,і , серед яких відокремимо дві основні:

·  симетрична стратегія  S₁(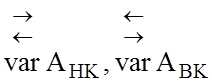), яка є виправданою, наприклад, за умови підтвердження розвідувальним аналізом збігання номінального значення  А₀ з теоретичним центром розсіювання значень навчальної вибірки  ;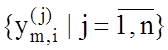

·  асиметрична стратегія  S₂(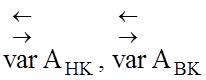), яка має місце при відхиленні значення  А₀   від центра розсіювання значень вибірки  .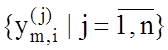

Задача оптимізації СКД на ознаки розпізнавання є частковою задачею інформаційного синтезу, в якій необхідно визначити екстремальні значення 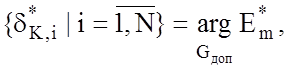  де   – область допустимих значень контрольних допусків. Згідно з діаграмою  відображень множин (2.4.3), в процесі навчання оптимізація СКД здійснюється за ітераційною процедурою, в якій задіяно оператори контура (2.4.5).

Розглянемо можливі алгоритми оптимізації СКД:

·  послідовний алгоритм, при якому контрольні допуски оптімізуються послідовно для кожної ознаки розпізнавання при фіксованих (стартових) значеннях інших ознак;

·  паралельний алгоритм, при якому контрольні допуски оптимізуються для всіх ознак одночасно;

·  алгоритм оптимізації за зведеним полем допусків.

При класифікаційному керуванні процесами, для яких словник ознак розпізнавання складається із груп і окремих ознак з різними шкалами виміру, доцільно застосовувати алгоритми послідовної або послідовно-паралельної оптимізації контрольних допусків. При розпізнаванні зображень за умови жорстких вимог до оперативності оброблення великих масивів відеоінформації виправданим є використання паралельного алгоритму оптимізації СКД. Алгоритм оптимізації контрольних допусків за зведеним полем допусків доцільно застосовувати як послідовно-паралельний алгоритм за наявності різних шкал виміру для окремих груп ознак розпізнавання.

Алгоритм оптимізації контрольних допусків, як і інших параметрів навчання нечіткого регулятора, за МФСВ полягає у наближенні глобального максимуму інформаційного критерію оптимізації до найбільшого його значення в області значень функції критерію. Тому важливого значення набуває дослідження збіжності такого алгоритму. Розглянемо збіжність алгоритму послідовної оптимізації контрольних допусків на ознаки розпізнавання. Введемо такі позначення: