Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 2

Опис структурної схеми базового алгоритму  навчання LEARNING наведено в додатку  Б. Якщо параметри навчання: оптимальні радіуси контейнерів {} і еталонні вектори-реалізації  {} є вхідними даними для алгоритму екзамену, то значення КФЕ та екстремальних оцінок асимптотичних точнісних характеристик вирішального правила використовуються для аналізу ефективності процесу навчання за обраним алгоритмом.

Таким чином, оскільки основною процедурою базового алгоритму за МФСВ, крім визначення оптимальних геометричних параметрів контейнерів класів розпізнавання, є обчислення інформаційного КФЕ навчання СК розпізнаванню образів, знаходження робочої області визначення його функції і пошук у робочій області глобального максимуму критерію, то він виступає як   батьківський об’єкт для всіх алгоритмів оптимізації просторово-часових параметрів навчання, які за методологією об’єктно-орієнтованого проектування [203] успадковують його методи з відповідним їх довизначенням.

4.2. Оптимізація геометричних параметрів контейнерів класів

розпізнавання

Розглянемо приклад побудови на етапі навчання оптимального контейнера для класу  . На рис. 4.1  для наочності схематично показано спроектовані на площину вершини 36 реалізацій класу  , які позначено символом  ²+²,  і 36 реалізацій найближчого сусіднього класу  , які позначено символом  ²Ú². Тут   – вершини еталонних векторів відповідних класів.

 

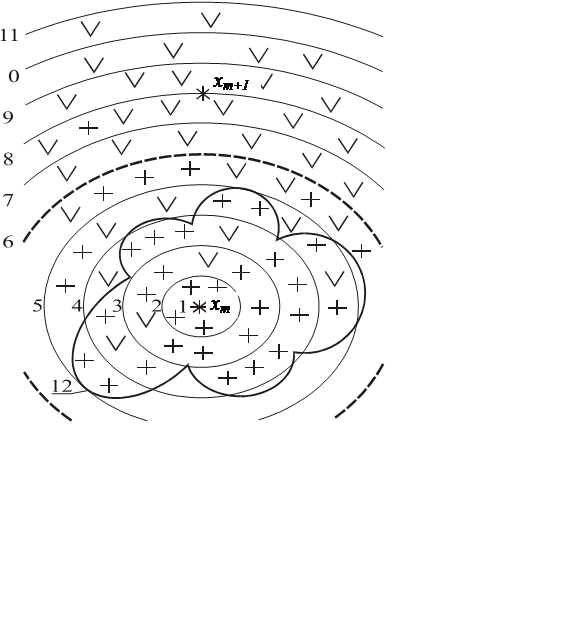Рис. 4.1. Розподіл реалізацій сусідніх класів    і 

У процесі навчання за алгоритмом (4.1.3) послідовно будувалися, згідно з процедурою (2.3.5), концентровані роздільні гіперсфери і на кожному  k-му кроці навчання обчислювалися за формулами  (3.5.2), (3.5.4) і (3.5.5) відповідно значення критеріїв  E_m ,   і  . При цьому коефіцієнти  і  обчислювалися за тестовим алгоритмом:

            

                    (4.2.1)

У табл.4.1 наведено значення точнісних характеристик і зазначених критеріїв, обчислених за базовим алгоритмом за одинадцять кроків навчання для розподілу реалізацій, показаному на рис. 4.1.

Таблиця 4.1

Результати оптимізації контейнера 

k	K1	K3	D1	a	D2	b	Em	Jm(g)	Jm
1	0	0	0,00	1,00	1,00	0,00	0,50	0,00	0,00
2	4	0	0,11	0,89	1,00	0,00	0,51	0,13	0,04
3	11	2	0,31	0,69	0,94	0,06	0,20	0,25	0,18
4	22	5	0,61	0,39	0,86	0,14	0,21	0,45	0,68
5	30	9	0,83	0,17	0,75	0,25	0,27	0,48	1,08
6	35	13	0,97	0,03	0,64	0,36	0,45	0,42	1,21
7	35	19	0,97	0,03	0,47	0,53	0,38	0,19	0,59
8	36	25	1,00	0,00	0,31	0,69	0,30	0,07	0,22
9	36	30	1,00	0,00	0,17	0,83	0,50	0,02	0,08
10	36	34	1,00	0,00	0,06	0,94	0,50	0,01	0,01
11	36	36	1,00	0,00	0,00	1,00	0,50	0,00	0,00
12	28	5	0,78	0,22	0,86	0,14	0,43	0,73	1,34