Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 3

Утабл.4.1 значення  К₁  дорівнює

кількості реалізацій класу  , що зна ходяться  в  k-й області, яку охоплює контейнер  . Відповідно  К₃  дорівнює кількості реалізацій сусіднього класу  , які охоплює контейнер  . Наприклад, для  k=3  в області    знаходиться 11 “своїх” і дві “чужих” реалізацій. Тому  (a⁽³⁾=0,69) і    ().

Аналіз точнісних характеристик за даними табл. 4.1 показує, що робочою областю визначення функцій розглянутих вище критеріїв оптимізації є область між значеннями  d_m=3  і  d_m=7, де помилки  a  і  b  менше відповідних достовірностей. При цьому оптимальний радіус контейнера для класу    за критерієм    дорівнює  =k- 1 = 5. Оптимальний контейнер за критерієм  J_m  має так само радіус  =5, а за критерієм  - =4. Таким чином, запропоновані модифікації критеріїв Шеннона і Кульбака дають у робочій області їх визначення однакові або близькі екстремальні значення їх аргументів. Зображена на рис. 4.2 область 12, яка побудована за критерієм максимуму правдоподібності за наведеною в праці [66] методикою, забезпечує максимальне відношенні “своїх” реалізацій до “чужих”. Порівняльний аналіз властивостей розглянутих модифікацій КФЕ за табл. 4.1 дозволяє зробити висновок про інваріантність КФЕ за Шенноном до критерію максимуму правдоподібності в той час як критерій Кульбака (загальний і частковий) є з ним корельованим, що пов’язано з його конструкцією. Оскільки значення запропонованих модифікацій Кульбака так само корельовані в процесі навчання за МФСВ із значеннями модифікації критерію за Шенноном (3.2.2), то можна зробити висновок, що критерій Кульбака є узагальненням ентропійного критерію Шеннона (3.1.1) і критерію Фішера [126], який за своєю суттю є критерієм правдоподібності.

Реалізацію базового алгоритмунавчання СК розглянемо на прикладі задачі оптимізації геометричних параметрів контейнера, яка має місце при автофокусуванні растрового електронного мікроскопа РЕМ-103 виробництва ВАТ “Selmi” (м.Суми, Україна) за зображенням зразка, що досліджується. Ідея автофокусування у рамках класифікаційного настроювання за МФСВ полягає у побудові на кожному кроці автофокусування оптимального контейнера    для початкового розфокусованого зображення (клас  ) відносно поточного зображення (клас  ), одержаного на  S-му кроці, і пошуку в процесі настроювання максимуму інформаційної міри різноманітності цих класів з метою визначення екстремального кроку  S^*. Як параметр настроювання розглядався струм управляючої обмотки об’єктивної лінзи, який програмно змінювався на кожному кроці за алгоритмом (2.7.2). На рис. 4.2а показано початкове розфокусоване зображення об’єкту «Кулі» (клас  ), а на рис. 4.2б - зображення цього об’єкту, яке отримано на  S-му кроці настроювання мікроскопа (клас  ).

                     а)                                                           б)

Рис. 4.2. Зображення об’єкту «Кулі»: а) початкове розфокусоване

зображення; б) поточне зображення

Формування навчальної матриці  ||||  здійснювалося шляхом сканування зображення    і виміру його яскравості в рецепторному полі розміром 51300 пікселів. При цьому за реалізацію зображення    приймалась крива розподілу яскравості в  j-му рядку рецепторного поля. Після визначення усередненої еталонної реалізації  y₁  було задано СКД, в якій поле допусків складало  d=40  градацій яскравості для всіх дискрет реалізації. Бінарна навчальна матриця 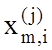 ||||  формувалася за правилом (4.1.1), а еталонний вектор  x₁ - за правилом (4.1.2) при рівні селекції  r₁=0,5. 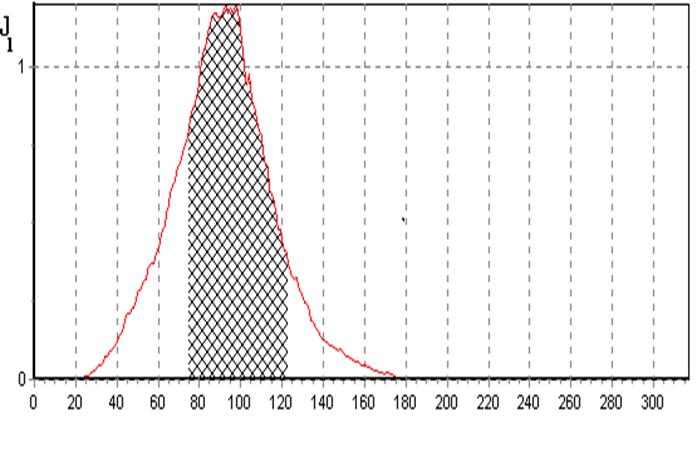Аналогічно оброблялось зображення  . На рис.4.3 показано залежність КФЕ за Кульбаком, який обчислювався за модифікацією (3.5.5), від радіуса  d₁. Тут штриховкою виділено робочу область визначення критерію  , в якій здійснюється пошук оптимального значення радіуса контейнера класу  .

d1