Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 18

Рис. 4.17. Розподіл реалізацій класу    за модифікованим алгоритмом

Порівняльний аналіз рис. 4.16 і рис. 4.17 показує, що, при модифікованому способі врахування реалізацій образу для обчислення коефіцієнтів    і  , емпіричний центр розсіювання реалізацій класу    наближається до геометричного центру контейнера  . При цьому забезпечується більше значення максимуму КФЕ  (рис. 4.17) у порівнянні із значенням максимуму критерію, обчисленного за процедурою (4.2.1). Це пов’язано з тим, що центрування контейнера    за модифікованим алгоритмом призводить до зменшення кількості “своїх” реалізацій, які знаходяться за межами контейнера, тобто до зменшення помилки першого роду. Відповідно, як витікає із процедур (4.91) і (4.9.2), при цьому збільшується перша достовірність    (збільшується коефіцієнт  ).

4.10. Аналіз та шляхи підвищення оперативності реалізації алгоритмів навчання за МФСВ

Якщо реалізація алгоритму екзамену за МФСВ здійснюється в реальному темпі часу, завдяки використанню в радіальному базисі відносно простих функцій належності для формування чітких керуючих висловлювань, то оперативність алгоритмів навчання змінюється у відносно широкому інтервалі часу залежно від повноти структури параметрів навчання (2.3.7), способу реалізації та видів самих алгоритмів навчання. При цьому підвищення оперативності алгоритмів навчання в рамках МФСВ доцільно здійснювати у двох напрямках:

·  пошук меж робочої області визначення функції інформаційного КФЕ навчання СК шляхом застосування алгоритмів оптимізації параметрів навчання із змінним кроком ітерації;

·  застосування оперативних алгоритмів пошуку глобального максимуму функції інформаційного КФЕ навчання безпосередньо в робочій області її визначення.

При підвищенні оперативності алгоритму навчання СК в рамках МФСВ за першим напрямком достатньо ефективними виявилися методи послідовного поділу навпіл допустимого інтервалу значень параметра оптимізації та зміна кроку навчання за оберненою послідовністю чисел  р-Фібоначчі [250], сума яких дорівнює інтервалу допустимих значень параметра  що є особливо виправданим при класифікаційному керуванні інерційними динамічними процесами. Так, для базового алгоритму навчання інтервал допустимих значень радіуса відповідного контейнера повинен бути менше міжцентрової відстані для двох сусідніх класів розпізнавання. Для алгоритмів оптимізації контрольних допусків на ознаки розпізнавання інтервал допустимих значень дорівнює полю відповідних нормованих допусків, які визначаються за наведеною в підрозділі 4.6. методикою.

Для підвищення оперативності алгоритмів навчання в рамках МФСВ за другим напрямком перспективним виявилося застосування генетичних алгоритмів пошуку глобального максимуму КФЕ навчання в робочій області визначення його функції, які відрізняються найбільшою оперативністю серед відомих алгоритмів. Якщо для базового алгоритму навчання використовувався стандартний генетичний елітарний алгоритм [112-114], то для оптимізації контрольних допусків розроблено специфічний генетичний алгоритм, в якому кросінговер здійснюється шляхом випадкової зміни параметра поля допусків    в робочій області визначення функції КФЕ навчання

Розглянемо кроки реалізації базового гібридного алгоритму навчання:

1. Формування бінарної навчальної матриці 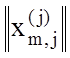 , елементи якої визначаються за правилом (4.1.1)

2. Формування бінарного масиву еталонних векторів-реалізацій образу , елементи якого визначаються за правилом (4.1.2)

3. Розбиття множини еталонних векторів-реалізацій образів на пари найближчих “сусідів”: , де   –еталонний вектор-реалізація, який має мінімальну кодову відстань до вектора , за алгоритмом, розглянутим і підрозділі 4.1.