Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 10

·    підготовчий етап;

·    формування зведеного поля допусків;

·  завдання стартових контрольних допусків для зведеного поля;

·    вибір стратегії зміни зведеного поля;

·    реалізація алгоритму оптимізації;

·  відображення за формулою (4.5.2) оптимальних значень зведеного поля допусків на шкали вхідних параметрів.

На підготовчому етапі здійснюють розбивку нормованих полів допусків вхідних змінних на градації і визначають їхню ціну. Вибір стартових значень нижнього    і верхнього   контрольних допусків на зведеному полі здійснюється за умови забезпечення випадковості реалізацій образу. Для зміни зведеного поля з метою пошуку екстремуму КФЕ на практиці достатньо обмежитися двома стратегіями. При цьому на кожному кроці оптимізації СКД за симетричною стратегією  S₁(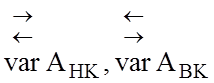) значення  і  одержують прирощення протилежного знаку, а за асиметричною стратегією  S₂(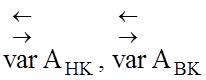)  значення    і    одержують прирощеня одного знаку. Таким чином, обов’язковими процедурами визначення оптимальної СКД на ознаки розпізнавання за МФСВ є обчислення за базовим алгоритмом інформаційного КФЕ на кожному кроці зміни зведеного поля за обраною стратегією і пошук у процесі навчання максимуму критерію в робочій області його визначення, що забезпечує максимальну асимптотичну достовірність класифікатора.

4.6. Визначення області значень контрольних допусків

При оптимізації процеса навчання СК за МФСВ важливим питанням є визначення системи нормованих допусків (СНД), яка задає області значень відповідних контрольних допусків на ознаки розпізнавання. Основні обмеження зверху (справа) на значення полів контрольних допусків    повинні забезпечувати:

·  збереження випадковості координат векторів-реалізацій образу;

·  недопущення збігання еталонних векторів, які є центрами відповідних контейнерів класів розпізнавання, що може призвести до невиконання умов як чіткого (2.3.2), так і нечіткого (2.3.4) розбиття простору ознак.

Як параметричні, так і непараметричні методи оцінки випадковості реалізацій образу обумовлюють наявність навчальної вибірки великого обсягу, що не завжди є здійсненим на практиці. Один із шляхів вирішення цієї проблеми ґрунтується на такій гіпотезі: чим більша середня кодова відстань між реалізаціями одного образу, тим більше вони будуть мати відмінних ознак розпізнавання, що свідчить про їх випадковість. Розглянемо постановку задачі оптимізації системи нормованих допусків, яка задає область визначення СКД, за дистанційно-максимиальним критерієм. Нехай   множина релізацій базового класу  {}, яку розіб’ємо на пари сусідніх векторів і визначимо кодові відстані між ними:

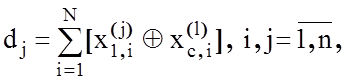                                                                   (4.6.1)

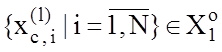де  – і-та координата реалізації  , яка є найближчою сусідньою до реалізації 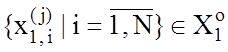 . Необхідно вибрати таку систему допусків  , щоб середнє вибіркове

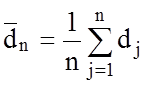                                                                                                (4.6.2)

відстані    для сусідніх реалізацій класу    було максимальним, тобто  ,  якщо  .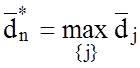

Таким чином, параметром, що оптимізується, є величина симетричного поля допусків  , центром якого є значення дискрети еталонної реалізації    базового класу  . Алгоритм складається із послідовного проведення етапів оптимізації, на кожному з яких формується при поточній СКД множина двійкових векторів-реалізацій , здійснюється її розбиття на пари сусідніх реалізацій за умови мінімальної кодової відстані між ними, обчислюється за формулою (4.6.2) середня кодова відстань для сусідніх реалізацій і здійснюється наступний крок ітераційної процедури пошуку максимуму  . Вхідні дані: 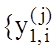|– масив дискрет реалізацій, що аналізуються, де  n_min – мінімальний обсяг репрезентативної навчальної вибірки, який обчислюється за методикою, наведеною в підрозділі 3.7;  - змінна поля допусків; h – крок зміни поля допусків,  l – змінна кроків ітерації. Результатом алгоритму оптимізації є поля нормованих допусків , які задають допустиму область значень контрольних допусків і цим забезпечують випадковість ознак розпізнавання.