Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 21

У табл.. 4.7  показано динаміку зміни параметрів навчання за алгоритмом послідовної оптимізації СКД на ознаки розпізнавання (4.4.1). При цьому як КФЕ навчання використовувалася ентропійна модифікація (3.5.2).

Таблиця 4.7

Значення параметрів навчання при послідовнійоптимізації СКД

LSKD	Клас				Клас
0	0,62106	30	0,72	0	0,68785	44	0,89	0,02	61
1	0,68325	32	0,81	0	0,88240	40	0,96	0	57
2	0,70102	28	0,83	0	0,90500	32	0,97	0	47
3	0,70102	27	0,83	0	0,93038	31	0,98	0	46
4	0,72069	23	0,85	0	1	27	1	0	40
5	0,79442	22	0,91	0	1	21	1	0	33
6	0,84309	22	0,94	0	1	21	1	0	34
7	0,88240	22	0,96	0	1	21	1	0	34
8	1	21	1	0	1	20	1	0	34
9	1	18	1	0	1	16	1	0	30
10	1	16	1	0	1	14	1	0	27
11	1	16	1	0	1	14	1	0	27

У табл. 4.7 нульовою ітерацією є знаходження стартової СКД на ознаки за паралельним алгоритмом. При цьому не виключається й апріорне їх завдання.

Динаміка зміни функціональної ефективності навчання ілюструється   рис. 4.23. Як видно з рис. 4.23 у результаті оптимізації СКД за алгоритмом (4.4.1) були отримані параметри навчання, що дозволили побудувати безпомилкове вирішальне правило без додаткової оптимізації інших параметрів функціонування, що входять в структуру (2.3.7). Подальше практичне застосування послідовного алгоритму оптимізації СКД на ознаки розпізнавання (4.4.1) показало його достатність за умови обґрунтування гіпотези одномодальності нечіткої компактності реалізацій образу, яка є характерною для переважної більшості практичних задач керування. При цьому, безумовно, задача підвищення оперативності навчання в рамках МФСВ повинна постійно знаходитися в полі зору розробника інформаційного забезпечення СК.

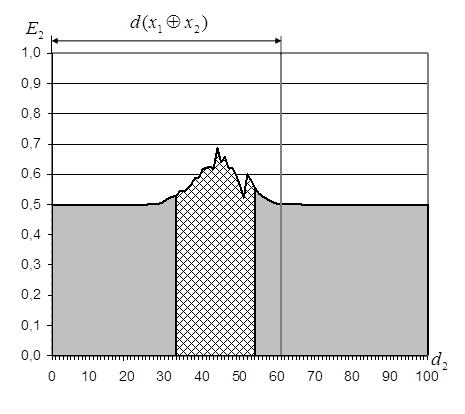
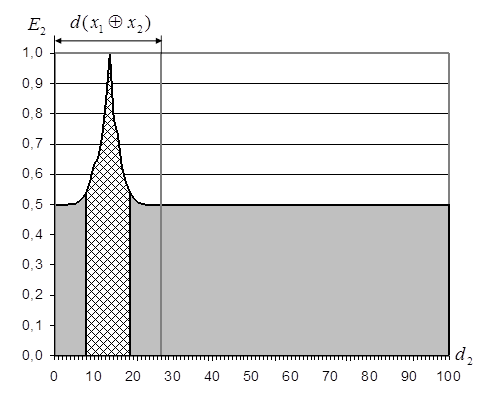
                              а)                                                                 б)

Рис. 4.23. Оптимізація радіуса контейнера класу  : а) для стартової СКД

(L_SKD =0); б) після останнього прогону алгоритму оптимізації СКД

Оперативність реалізації даного алгоритму можна оцінити через кількість ітерацій, максимальне значення яких за формулою (4.10.1) дорівнює 22 183 524 (при N_D=N) та скорочується до 8 387 344 при використанні обмеження (2.3.6). Це досить суттєве зменшення можна пояснити тим, що вже після нульової ітерації центри контейнерів класів розпізнавання знаходяться на кодовій відстані 61 один від одного (максимальна можлива відстань складає 100), а в процесі оптимізації міжцентрова відстань зменшується до 27 (Табл. 4.2).

Слід зазначити що, крім зменшення міжцентрової відстані зменшується так само і робоча область, яка позначена на рис 4.  заштрихованою ділянкою. При застосуванні алгоритму навчання за методом прямого пошуку межі робочої області визначаються в процесі оптимізації на кожній ітерації. Але аналіз динаміки зміни її параметрів дозволяє встановити додаткові обмеження на область пошуку оптимальних параметрів навчання: