Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 13

Розглянемо вплив рівня селекції на ефективність навчання СК при розв’язання задачі центрування контейнерів класів розпізнавання. Оптимізацію рівнів селекції    будемо здійснювати в рамках алгоритму навчання за МФСВ. Нехай дано – алфавіт М класів розпізнавання, які можуть перетинатися, і навчальну матрицю 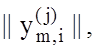   де  - кількість ознак і реалізацій образу відповідно. Відомий вектор параметрів навчання   з обмеженнями  . Треба на етапі навчання побудувати в бінарному просторі ознак  W_Б  оптимальне в інформаційному розумінні нечітке розбиття    і при цьому визначити оптимальні значення параметрів, які забезпечують максимум критерію функціональної ефективності (КФЕ) навчання:

,

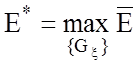де 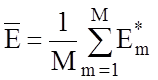     – усереднений КФЕ навчання;

          - області допустимих значень параметрів навчання.

          Тут  – максимум КФЕ навчання розпізнаванню реалізацій класу  . Тоді за виразом (2.3.8) структурований алгоритм оптимізації рівня селекції для пари найближчих класів    і    має вигляд:

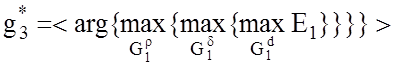                             ,                              (4.7.2)

де      області допустимих значень відповідних параметрів навчання для класу  .

          При цьому внутрішній цикл алгоритму (4.7.2) реалізується послідовно операторами, які утворюють базовий контур (2.4.2). Наступний цикл реалізується послідовністю операторів контуру оптимізації СКД (2.4.5) і зовнішній цикл - послідовністю операторів контуру оптимізації рівнів селекції (2.4.4) у діаграмі (2.4.3).

          Для ілюстрації реалізації алгоритму (4.7.2) розглянемо задачу побудови контейнера класу    із застосуванням процедури оптимізації рівня селекції координат вектора    при визначенні інформаційної міри різноманітності між початковим базовим класом    і поточним класом    у процесі автофокусування електронного мікроскопа РЕМ-103 за зображенням зразка, що досліджується. На рис.4.9а наведено початкове розфокусоване зображення об’єкту «Гратка» (клас  ), а на рис.4.9б - зображення цього об’єкту, отриманого на  S-му кроці настроювання (клас  ).

         

                               а)                                              б)

Рис. 4.9. Зображення об’єкту «Гратка»: а) початкове розфукусоване зображення; б) поточне зображення.

У процесі реалізації алгоритму навчання як критерій оптимізації використовувалася модифікація (3.5.2) і було побудовано отимальний контейнер  , радіус    якого, як видно з рис. 4.10, дорівнює 35 одиницям кодової відстані при значенні КФЕ  .  

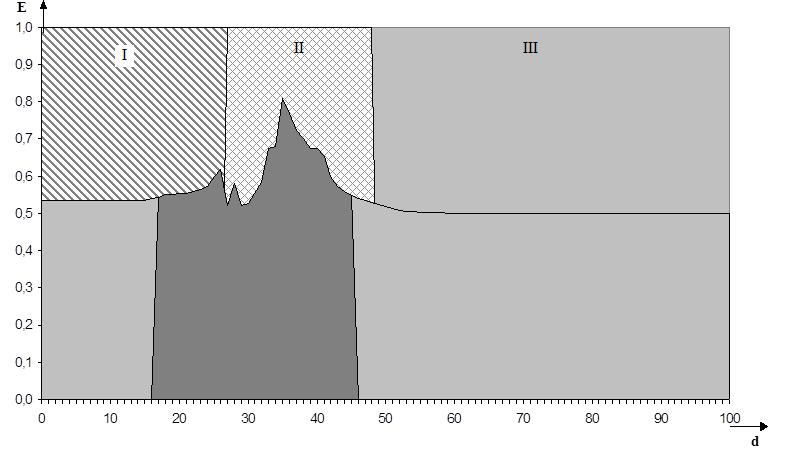
Рис. 4.10. Залежність КФЕ від радіуса контейнера 

На рис.4.10 найбільш темна область графіка позначає робочу область визначення функції (3.5.2). В області І присутні тільки реалізації класу , в області перетину ІІ присутні реалізації класів    і  , а в області  ІІІ - тільки реалізації класу  .

У табл. 4.4 наведено значення критерію  Е₁  першої достовірності    і помилки другого роду  b, параметрів навчання  r₁,    і міжцентрова кодова відстань  _. Як видно з табл. 4.5, оптимальне значення рівня селекції дорівнює  , а оптимальне поле контрольних допусків для і-ї ознаки дорівнює  , де  d^*=12 градаціям яскравості. Незважаючи на те, що при  r₁=0,54  значення  критерію  Е₁  таке саме як і при  r₁ = 0,56, за оптимальне приймається рівень  , оскільки він  забезпечує більшу міжцентрову відстань  .

Таблиця 4.4

Результати оптимізації контейнера