Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 12

k
	13	2	3	5	2	4	2
	2	13	3	3	2	4	2
	3	3	13	4	3	3	3
	5	3	4	13	5	6	5
	2	2	3	5	13	4	2
	4	4	3	6	4	13	2
	2	2	3	5	2	2	13

За табл. 4.3 визначимо за алгоритмом, наведеним у підрозділі 4.1, пари сусідніх векторів: =<,>, =<,>, =<,>, =<,>, =<,>,  =<,>,  =<,>. Відповідно кодові відстані між сусідніми векторами дорівнюють: d()=2; d()=2; d()=3; d()=3; d()=2; d()=2; d()=2.

На рис. 4.8 наведено залежність середньої кодової відстані    (4.6.2)  від параметра    поля допусків.

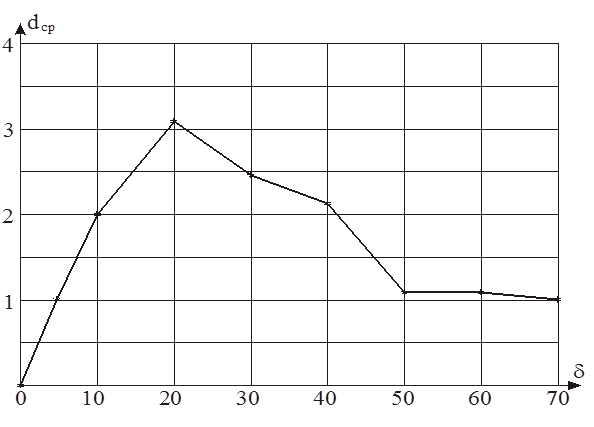
Рис. 4.8. Залежність середньої кодової відстані   від величини поля

допусків

Аналіз рис. 4.8 показує, що область визначення СКД на ознаки розпізнавання задається оптимальним значенням відповідних полів нормованих допусків 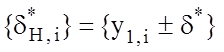 , де  , які гарантують випадковість реалізацій образу, згідно з принципом рандомізації вхідних даних у МФСВ. При цьому система нормованих допусків знизу обмежується вимогою виключення переходу реалізацій образу в нульові. Так, вже при    перша, друга і шоста реалізації стають нульовими. З іншого боку, при збільшенні параметра  до 70 збігаються друга та четверта реалізації, що робить подальше збільшення нормованого поля недоцільним. Невдалий вибір області визначення СКД на ознаки може суттєво вплинути як на точнісні характеристики СПР, так і на оперативність навчання. Так, вибір занижених нормованих полів допусків призводить до погіршення точнісних характеристик класифікатора, а вибір завищених – до зменшення оперативності навчання. Таким чином, розробка ефективних критеріїв оцінки випадковості навчальної вибірки в рамках МФСВ набуває важливого значення.

4.7. Оптимізація рівнів селекції координат еталонних двійкових

векторів-реалізацій образу

Оскільки рівень селекції  ,  безпосередньо впливає на координати еталонних двійкових векторів, вершини яких є геометричними центрами класів розпізнавання, то його цілеспрямована зміна, в рамках ітераційних процедур оптимізації параметрів функціонування СК за МФСВ, дозволяє розв’язувати такі важливі для підвищення достовірності класифікації задачі:

·  центрування контейнерів класів розпізнавання;

·  максимізація середньої міжцентрової кодової відстані для заданого алфавіту класів розпізнавання;

·  оцінка інформативності ознак розпізнавання.

Проблема центрування контейнерів пов’язана з використанням на практиці навчальної вибірки малого обсягу (n<1000), що обумовлює появу статистичної похибки між емпіричною частотою    та ймовірністю    знаходження значення  і-ї ознаки в своєму полі контрольних допусків. Це обумовлено тим, що вершина двійкового вектора  , координати якого визначаються шляхом статистичного усереднення значень відповідних ознак розпізнавання, не збігається з теоретичним центром розсіювання реалізацій класу . Необхідність максимізації середньої міжцентрової кодової відстані для алфавіту класів :

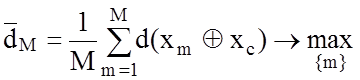                                                                 (4.7.1)

у МФСВ обумовлена тим, що функції статистичних інформаційних критеріїв оптимізації параметрів функціонування СК не є взаємно-однозначними. Оскільки рівень селекції впливає на міжцентрову відстань пари сусідніх векторів, то вибір його оптимального значення із множини екстремальних значень доцільно здійснювати саме за дистанційно-максимальним критерієм (4.7.1). Визначення оптимального рівня селекції дозволяє змінювати потужність словника ознак розпізнавання. Так, якщо виявилося, що ознаки, які за умовчанням ( мали нульові координати в еталонному векторі, при  перейшли в одиничні координати, то вони є латентними. Якщо ознаки при   поміняли одиничні координати на нульові, то вони є кандидатами на виключення із словника як “заважаючі”.