Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 19

4. Пошук меж робочої області визначення функції інформаційного КФЕ навчання СК за методом половинного поділу інтервалу визначення параметру оптимізації, При цьому критерієм виявлення лівої межи робочої області є виконання умови 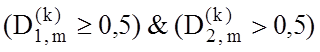 , а для виявлення правої межи – .

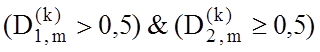5. Оптимізація кодової відстані    за стандартним генетичним алгоритмом [246,247]

5. Процедура закінчується при знаходженні максимуму КФ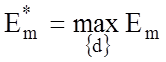Е , де  – множина радіусів концентрованих гіперсфер, центр яких визначається вершиною вектора  .

6. Визначення оптимального радіусу контейнера класу  : .

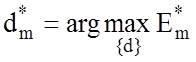Для ілюстрації роботи базового гібридного алгоритму навчання за МФСВ розглянемо побудову контейнерів для двох (М=2) стаціонарних за яскравістю зображень, отриманих на растровому мікроскопі РЕМ-103 і показаних на рис. 4.18.

                 

                                              а)                                                  б)

Рис. 4.18. Зображення: а) клас  ; б) клас  .

На рис. 4.19 показано результат оптимізації радіуса контейнера класу , а на рис. 4.20 – радіуса  контейнера класу   в рамках базового алгоритму навчання за методом прямого пошуку глобального максимуму КФЕ навчання, який обчислювався за модифікацією (3.5.5) при   .

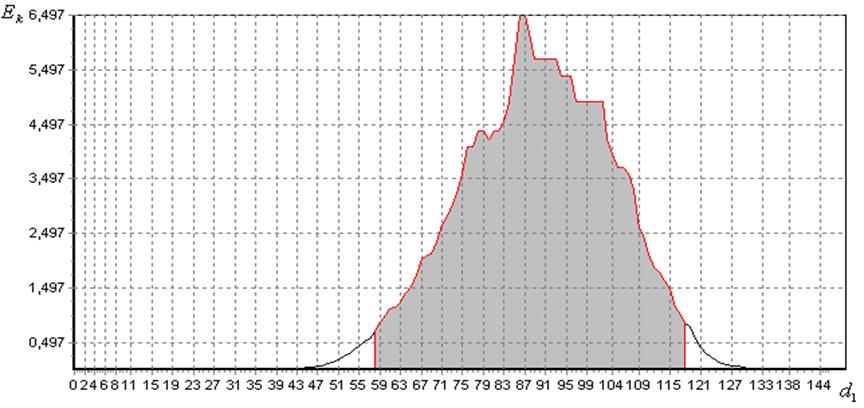
Рис. 4.19. Визначення оптимального радіуса контейнера класу    в рамках

базового алгоритму навчання за методом прямого пошуку

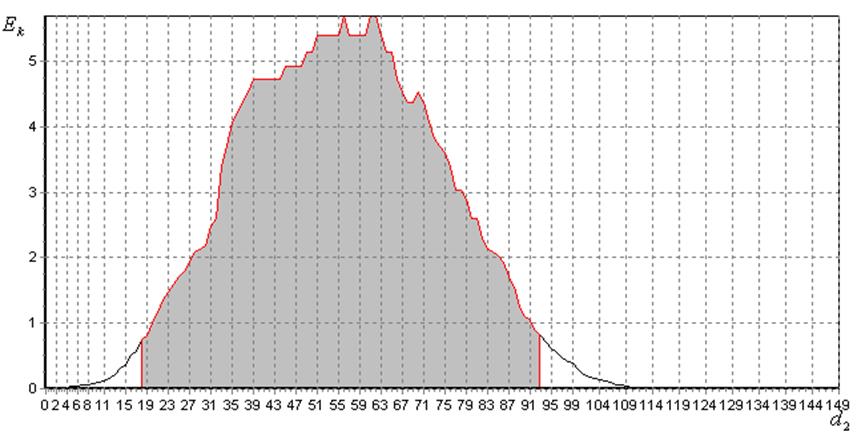
Рис. 4.20. Визначення оптимального радіуса контейнера класу  в рамках

базового алгоритму навчання за методом прямого пошуку

Результати реалізації базового гібридного алгоритму навчання за МФСВ показано на рис. 4.21 (клас  ) і на рис. 4.22 (клас  ). На цих рисунках дискретами в робочій області визначення функції критерію (3.5.5 ) позначено кроки навчання, на яких застосовувався генетичний алгоритм у відповідності з механізмом випадкового пошуку. Тобто , на відміну від методу прямого пошуку глобального максимуму КФЕ при застосуванні генетичного алгоритму значення критерію оптимізації обчислювалися не для всіє множини значень параметра в робочій області його значень.

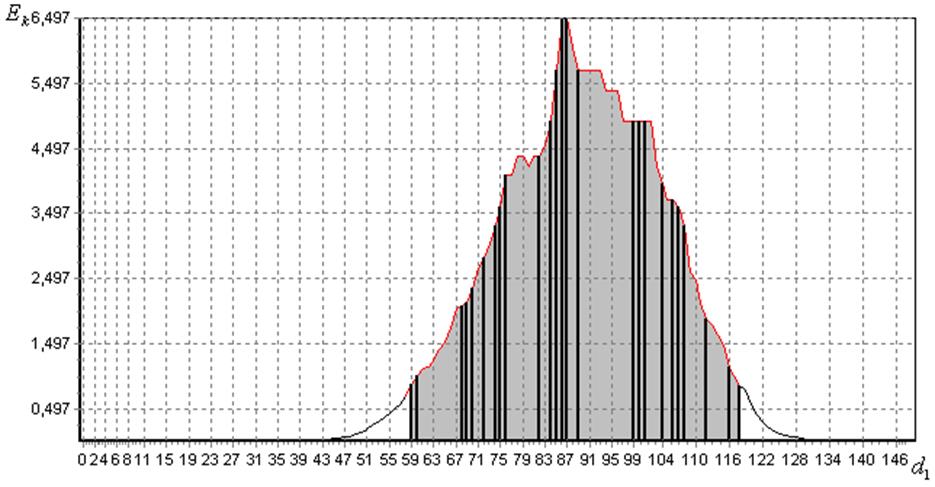
Рис. 4.21. Визначення оптимального радіуса контейнера класу    в рамках

базового алгоритму навчання за гібридним алгоритмом

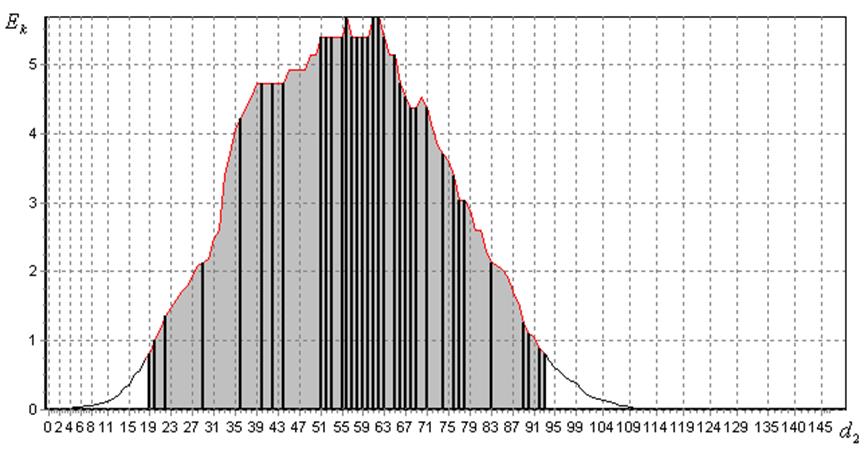
Рис. 4.22. Визначення оптимального радіуса контейнера класу    в рамках

базового алгоритму навчання за генетичним алгоритмом

Порівняння точних меж робочих областей визначення функції КФЕ     (рис. 4.19 і рис. 4.20) з відповідними межами робочих областей, одержаних за методом половинного поділу інтервалу визначення параметрів оптимізації (рис. 4.21 і рис. 4.22), який дорівнює  кодовим одиницям, показує, що їх абсолютна похибка становить менше одного відсотка, що для практичних задач не є суттєвим, оскільки глобальний максимум КФЕ навчання ніколи не знаходиться на межі робочої області визначення його функції, що витікає безпосередньо із твердження  2.3.4.   

У процесі дослідження була написана програма тестування стандартного генетичного алгоритму [246,247], а за результатами тестування визначено оптимальні вхідні параметри алгоритму (табл. 4.6).

                                                                                                           Таблиця 4.6

Оптимальні параметри генетичного алгоритму