Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 22

·  верхня межа робочої області не зростає в процесі оптимізації, тобто її значення на попередній ітерації можна використовувати як кінцеве значення на наступній ітерації при оптимізації радіусів контейнерів класів навчання замість міжцентрової відстані;

·  на початку оптимізації кількість ітерацій, що відповідають області від центру контейнера поточного класу до нижньої (лівої) межи робочої області, складає досить вагому частину від загальної кількості ітерації. Це вказує на необхідність зміни напрямку ітераційного процесу замість збільшення значення радіуса від нуля до верхньої межи, слід зменшувати його значення від верхньої межи до моменту виходу з робочої області.

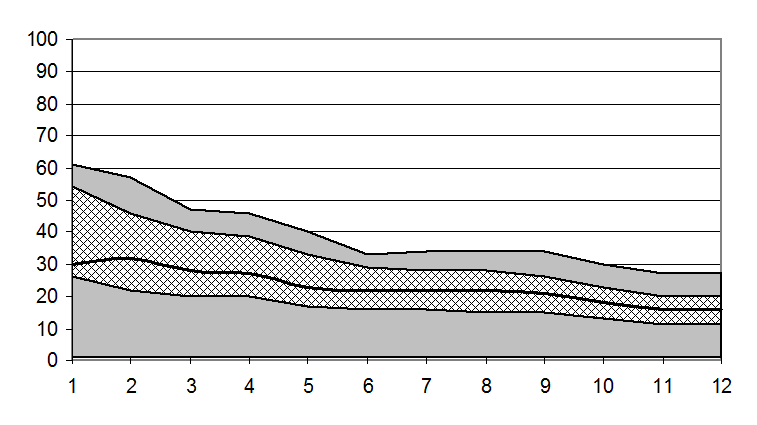
Динаміку зміни робочої області визначення функції КФЕ навчання в процесі реалізації алгоритму (4.4.1) показано на рис.4.24 і 4.25.

 

L

Рис. 4.24. Зміна параметрів робочої області при оптимізації

контейнера класу 

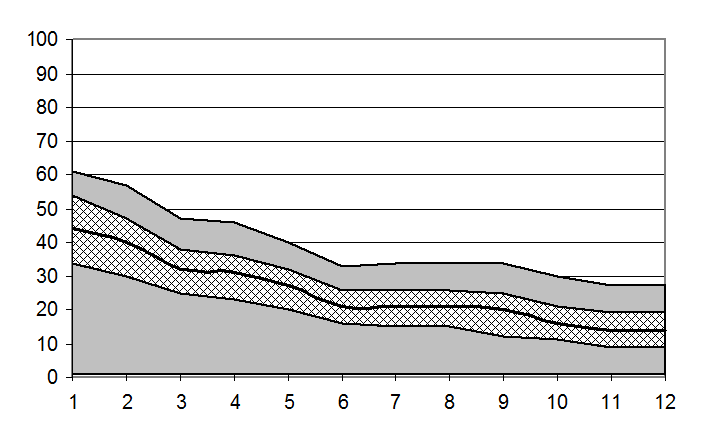
Аналіз рис. 4.24 і 4.25 показує, що в процесі оптимізації параметрів навчання за алгоритмами в рамках МФСВ відбувається зменшення як радіуса контейнера відповідного класу (на рисунках– чорна крива), так і робочої області визначення глобального максимуму функції КФЕ навчання. Зменшення радіуса контейнера означає, що в процесі цілеспрямованої трансформації розподілу реалізацій образу на кожному кроці навчання зменшується середня відстань між реалізаціями свого образу, тобто відбувається перехід нечіткого розбиття простору ознак в чітке. Моментом такого переходу є крок навчання, на якому інформаційний КФЕ набуває максимального значення в робочій області визначення його функції, що означає відсутність у відновлених у процесі оптимізації контейнерах класів розпізнавання реалізацій інших класів.

 

                L

Рис. 4.25. Зміна параметрів робочої області при оптимізації

контейнера класу 

Таким чином, на відміну від відомих методів автоматичної класифікації синтезований за МФСВ нечіткий регулятор СК дозволяє в режимі екзамену приймати високо достовірні рішення в реальному темпі часу за умов нечіткої компактності реалізацій образу та мінімального обсягу репрезентативної  навчальної вибірки. Обсяг навчальної вибірки, за якою МФСВ забезпечує побудову безпомилкового вирішального правила, є більш ніж на порядок меншим у порівнянні з даними, наведеними при реалізації статистичних методів розпізнавання образів у праці [119], де  . Можливість використання в МФСВ навчальних вибірок  супермалих  обсягів  пояснюється як застосуванням логарифмічних статистичних інформаційних КФЕ навчання, переваги яких відмічено в працях А.А. Колмогорова [251] і О.А. Борисенка [174], так і наявністю в МФСФ механізму статистичної корекції вирішального правила. Розглянуті вище специфічні та відомі способи [252-255] і шляхи підвищення оперативності навчання за МФСВ відкривають перспективу широкого використання запропонованої методології проектування інформаційного забезпечення СК, що навчаються, в різних галузях соціально-економічної сфери України.

4.11. Висновки до четвертого розділу

Таким чином, у четвертому розділі розроблено алгоритми оптимізації парамерів навчання СК і досліжено їх вплив на функціональну ефективність процесу навчання, яка визначає асимптотичні точнісні характеристики нечіткого регулятора. У результаті проведених досліджень і машинних експерементів отримано такі результати:

1.  У рамках МФСВ оптимізація СКД на ознаки розпізнавання є обов’язковою процедурою, яка реалізується після виконання базового алгоритму навчання. Оптимальна базова СКД, яка прив’язується до значень ознак еталонного вектора  , де  - базовий клас розпізнавання, утворює у N-вимірному просторі коридор, відносно якого визначається міра різноманітності для всіх класів. Показано, що алгоритм послідовної оптимізації СКД на ознаки розпізнавання збігається з імовірністю одиниця, а алгоритм паралельної оптимізації СКД – за імовірністю.