Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 17

                                         .                        (4.9.1)

       Для випадку    алгоритм такий:

                                          .                       (4.9.2)

З метою порівняльного аналізу ефективності алгоритмів (4.9.1) і (4.9.2) розглянемо знову оптимізацію геометричних параметрів контейнера за МФСВ на прикладі автофокусування растрового електронного мікроскопа РЕМ-103 за зображеннями зразка, що досліджується. За вихідні приймемо зображення, що наведено на рис. 4.9. Ітераційний процес пошуку максимуму інформаційного КФЕ обумовлює необхідність його максимізації на кожному кроці настроювання мікроскоппа, що дозволяє однозначно порівнювати значення критерію. При цьому відновлений за алгоритмом навчання у рамках МФСВ оптимальний контейнер    класу   забезпечує максимальну різноманітність початкового та поточного зображень. Оскільки в задачі автофокусування зображення зразка, що досліджується, на кожному кроці настроювання є стаціонарними за яскравістю, то формування бінарних навчальних матриць і еталонних векторів-реалізацій для початкового і поточного класів здійснювалося так само за правилами (4.1.1) і (4.1.2). Як параметри навчання приймалися радіус   контейнера   і  параметр    поля контрольних допусків на ознаки розпізнавання. Отже, алгоритм навчання за МФСВ становив двоциклічну ітераційну процедуру пошуку максимуму критерію  :

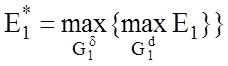                                                    ,                                         (4.9.3)

де      – допустима область значень параметра  :  ;

–  допустима область значень радіуса контейнера класа  :  .

          У процедурі (4.9.3) оптимізація параметрів    і   здійснювалася за паралельним алгоритмом оптимізації контрольних допусків на ознаки розпізнавання LEARNING-2.

На рис. 4.14 показано залежність КФЕ навчання, що обчислювався за формулою (3.5.2) згідно з немодифікованою процедурою (4.2.1), від радіуса контейнера  , а на рис. 4.15 – таку саму залежність цього критерію, що обчислювався за модифікованими процедурами (4.9.1) і (4.9.2). При цьому оптимальне значення параметра поля контрольних допусків на ознаки розпізнавання дорівнювало    градацій яскраваості.

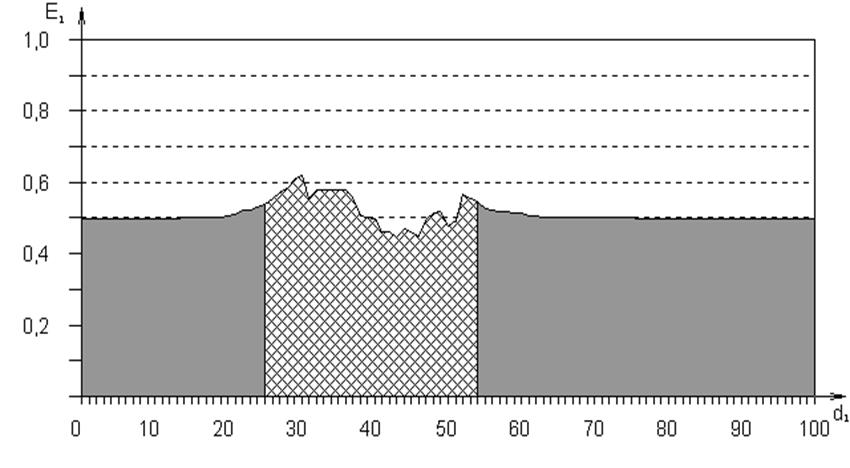
Рис. 4.14. Залежність КФЕ від радіуса контейнера    для немодифікованої процедури (4.2.1)

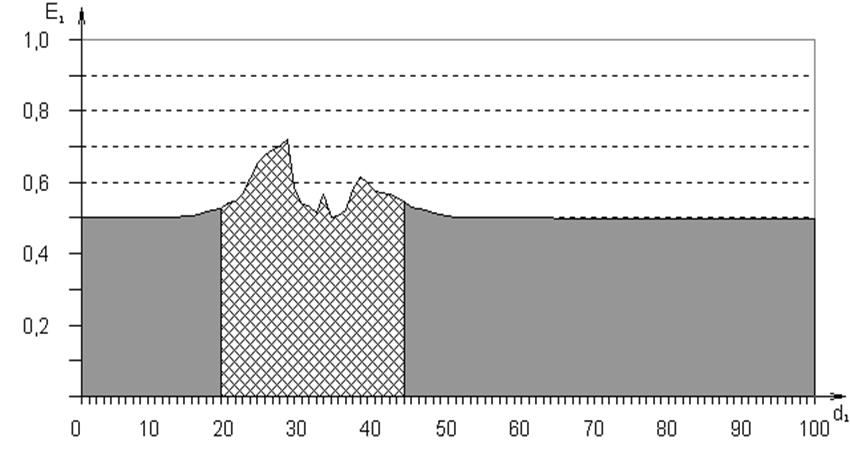
Рис. 4.15. Залежність КФЕ від радіуса контейнера    для

модифікованої процедури

На цих рисунках подвійною штриховкою позначено робочі області визначення КФЕ навчання. Оптимальний радіус    контейнера  , як видно з рис. 4.14, дорівнює 29 кодовим одиницям відстані при значенні КФЕ  . Відповідно на рис. 4.15 –  при  значенні КФЕ  , що свідчить про ефективність запропонованої модифікації.

Для пояснення підвищення ефективності навчання за модифікованим алгоритмом обчислення КФЕ навчання проаналізуємо трансформацію розподілу реалізацій класу  , який має місце при застосуванні процедури (4.2.1) і відповідно процедур (4.9.1) і (4.9.2). Розглянемо гомоморфне відображення вершин векторів-реалізацій класу    на площину  . Для визначення на площині координат  реалізації   необхідно розв’язати систему рівнянь:

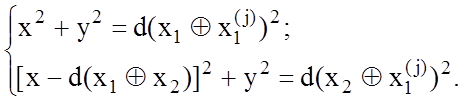
Звідки такі координати дорівнюють:

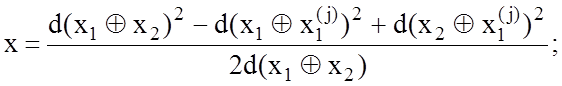
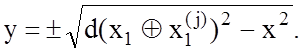
На рис. 4.16 показано розподіл реалізацій класу  , який має місце  при обчисленні інформаційного КФЕ за процедурою (4.2.1). Всього розглядалося 100 реалізацй кожного класу, які зображено на рис. 4.16 точками. При цьому координати деяких реалізацій збігалися. Аналіз розподілу реалізацій на рис. 4.16 показує, що центр розсіювання реалізацій класу  , який  дорівнює середньому вибірковому реалізацій свого класу, зміщено відносно геометричного центру контейнера   (на рис. 4.16 його показано зліва).

Рис. 4.16. Розподіл реалізацій класу   за процедурою (4.2.1)

На рис. 4.17 показано розподіл реалізацій класу    при застосуванні для обчислення КФЕ навчання  процедур (4.9.1) і (4.9.2).