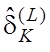Оптимізація просторово-часових параметрів функціонування системи керування, що навчається, страница 7

– екстремальне значення параметра поля контрольних допусків, де  L– крок зміни поля допусків, при якому КФЕ навчання досягає глобального значення   ;

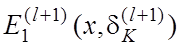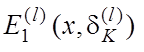Розглянемо послідовність  , де L –крок зміни параметра  , на якому  КФЕ навчання досягає значення   і –. Тут   – будь-яке мале додатнє число.

Тоді має місце таке твердження:

Т в е р д ж е н н я  4.4.2. Послідовність    при збільшенні параметра    до величини    монотонно спадає і обмежена знизу.

Як витікає із твердження 2.3.4 інформаційний КФЕ, який є функціоналом від точнісних характеристик, має в робочій області його визначення глобальний максимум (за допущенням при  ), тому при    твердження 4.4.2 має місце.

Т е о р е м а 4.4.2. Алгоритм паралельної оптимізації контрольних  допусків на ознаки розпізнавання збігається за ймовірністю, тобто 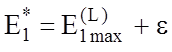 , де   – будь-яке мале додатнє число.

Для доведення цієї теореми достатньо показати, що послідовність   не є стаціонарною, тобто , оскільки екстремальний параметр 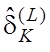 , по крайній мірі, для однієї ознаки розпізнавання не є оптимальним.

Розглянемо схему алгоритму LEARNING-1, призначеного для послідовної оптимізації контрольних допусків на ознаки розпізнавання за процедурою (4.4.1). Вхідні дані: масив реалізацій образу  ; стартова СКД   і система нормованих допусків (СНД)  , яка визначає область значень відповідних контрольних допусків. Стартовий параметр    поля контрольних допусків може дорівнювати половині відповідного симетричного поля нормованих допусків для і-ї ознаки за умови випадковості її значень. Попередньо для кожної ознаки визначається ціна градації  , на яку змінюється  і-та ознака.

Схема алгоритму послідовної оптимізації контрольних допусків така:

1.  Обнуління лічильника прогонів процедури оптимізації параметрів навчання: l:=0.

2.  Для стартової системи допусків обчислюється за базовим алгоритмом навчання  LEARNING  значення функції .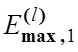

3.  Формування лічильника прогонів: l: l+1.

4.  Обнуління лічильника ознак розпізнавання: і:=0.

5.  Формування лічильника ознак розпізнавання: і: і+1.

6.  Визначення екстремального значення параметра 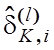   за процедурою (4.4.1), в якій внутрішній цикл оптимізації реалізує базовий алгоритм  LEARNING.

7.  .

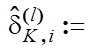
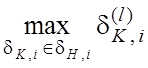8.  Якщо  , то виконується пункт  5, інакше пункт 9.

9.  Якщо 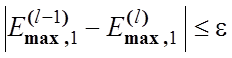 , де – будь-яке мале позитивне число, то виконується пункт 10, інакше пункт 3.

10. 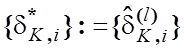 і “Зупин”.

Приклад реалізації алгоритму послідовної оптимізації ознак розпізнавання наведено в сьомому розділі.

Паралельний алгоритм  LEARNING-2  оптимізує параметри контейнерів класів розпізнавання за умови ітераційної процедури визначення для базового класу    оптимальних контрольних допусків на всі ознаки одночасно. Вхідні дані такі самі як і для алгоритму  LEARNING-1, але за область визначення параметра    приймається інтервал  , де  - ширина нормованого поля допусків. Розглянемо кроки реалізації цього алгоритму:

1.  Обнулюється лічильник кроків зміни параметра  : l:=0.

2.  Запускається лічильник: l:=l+1  і обчислюються нижні та верхні контрольні допуски для всіх ознак:  і  ,  відповідно.

3.  Реалізується базовий алгоритм навчання.

4.  Якщо , то виконується пункт 5, інакше пункт 6.

5.  Якщо  , то виконується пункт 2, інакше пункт 6.

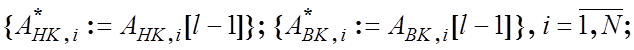
6.    і “ЗУПИН”.

Розглянемо приклад паралельної оптимізації СКД в процесі автофокусування растрового електронного мікроскопа РЕМ-103 за наведеними на          рис. 4.2 зображеннями зразка, що досліджувався. На кожному кроці настроювання для поточного значення  , яке збільшувалося на одиницю, обчислювався критерій оптимізації за формулою (3.5.5) і визначалось оптимальне значення радіуса контейнера базового класу  . 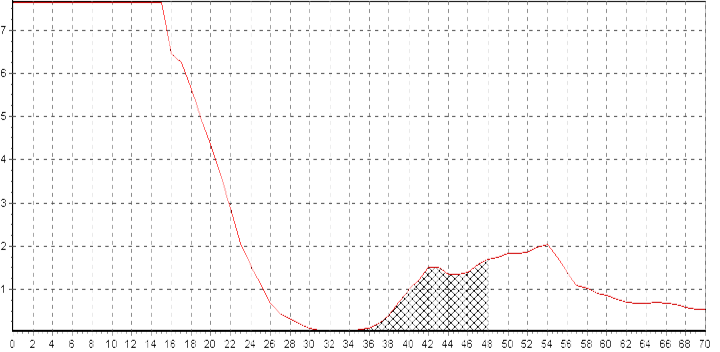На рис. 4.5 наведено залежність модифікації критерію Кульбака від параметра    в процесі навчання за алгоритмом  LEARNING-2.

J₁

d

Рис. 4.5. Залежність КФЕ від параметра поля допусків

На рис. 4.6 показано залежність КФЕ від радіуса контейнера класу   для оптимального значення  , яке є максимальним в робочій області на рис. 4.5.