Глава 1. Общий характер городского радиоканала
При разработке и проектировании цифровых систем связи в условиях крупного города возникает необходимость построения модели канала связи. Модель канала связи должна включать в себя тип аддитивных помех, характер поля как около передающих антенн, так и около приемных антенн, то есть анализу подлежит модель непрерывного канала связи. При этом следует иметь в виду и характеристики цифрового модема.
Представим сигнал, приходящий на приемную антенну с круговой диаграммой направленности в виде
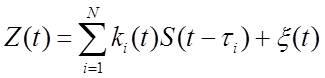 (1.1)
(1.1)
где ki(t) – амплитуда i-луча,
τi – задержка i-луча,
N – число лучей в месте приема.
ξ(t) – аддитивная помеха, имеющая плотность распределения вероятностей.
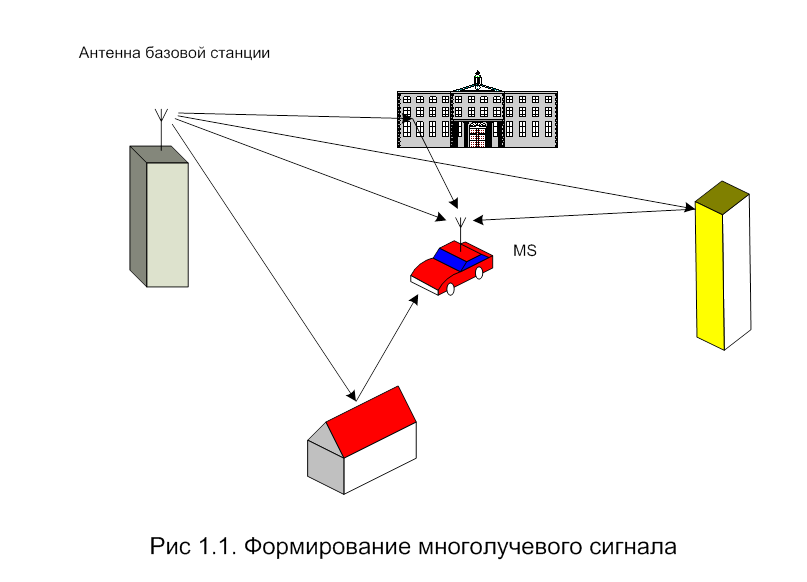
Модель канала (1.1) характеризует многолучевость распространения радиоволн, при этом анализу подлежит характер поведения всех ее компонентов в зависимости от характера застройки, высоты антенн, параметров цифровой модуляции. При τi << Т, где Т – длительность посылки сигнала, рассеяния по частоте нет, таким образом, канал характеризуется общими замираниями, когда все частотные составляющие спектра сигнала в одинаковой степени изменяются во времени.
Рассмотрим различные модели флуктуаций амплитуды сигналов в системах мобильной связи. Для различной застройки, разного количества лучей в месте приема и подвеса антенн будет иметь место случай: одна передающая антенна и одна приемная антенна, аддитивные помехи учитываться не будут.
Рассмотрим интерференционную модель канала. Сигнал в месте приема представлен как:
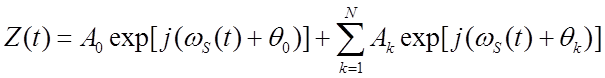 (1.2)
(1.2)
где А0 – амплитуда основного луча,
Ак – амплитуда k-луча,
θ0, θк – фазы основного и k-го лучей,
N – число переотраженных лучей.
Для
определения характеристик сигнала (1.2) перейдем к анализу напряженности поля Е,
которые образуются при сложении N взаимонезависимых плоских
волн с равномерным на интервале (0 ÷ 2π) законом плотности вероятностей,
распределением фазы 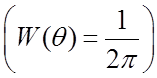 и произвольно распределенными
амплитудами, при этом воспользуемся [1], на основании которого справедливо
выражение:
и произвольно распределенными
амплитудами, при этом воспользуемся [1], на основании которого справедливо
выражение:
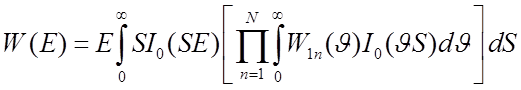 (1.3)
(1.3)
где I(z) – функция Бесселя первого рода нулевого порядка,
W1n – одномерная плотность вероятностей амплитуды n-й волны.
Вероятность того, что величина E превысит значение Е0
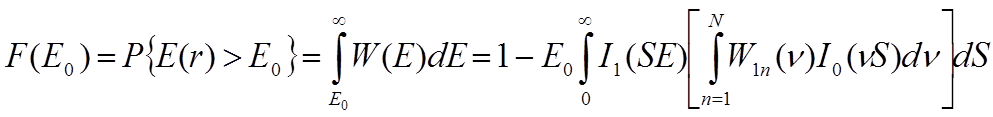 (1.4)
(1.4)
где I1(z) – функция Бесселя первого рода первого порядка
Число лучей многолучевого поля зависит от характера застройки и высот подвеса антенн.
Рассмотрим случай для N = 2, который характерен для высоко поднятой передающей антенны и низкоподнятой приемной антенной (1,5-3)м, застройка при этом - средней этажности. Для N = 2 характерны наибольшие замирания.
Для двухлучевой модели канала N = 2 амплитуды Епр и Еотр полагают постоянными. Плотности вероятностей для них W1 = δ( ν-Eпр), W2 = δ( ν-Eотр). Подставим эти функции в (1.3) и в (1.4), тогда для суммарного поля плотность вероятностей
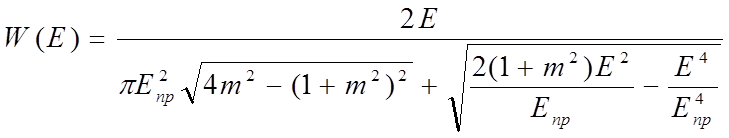 (1.5)
(1.5)
а функция распределения
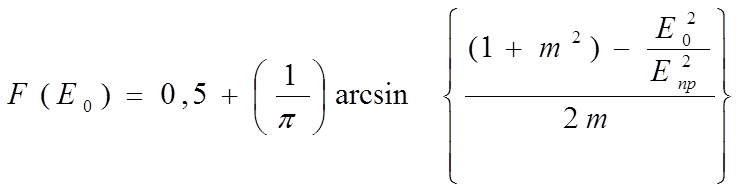 (1.6)
(1.6)
где
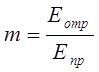
Еотр – амплитуда отраженной волны
Епр – амплитуда прямой волны
Математическое ожидание и дисперсия соответственно равны:
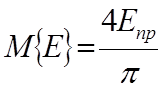 ;
; 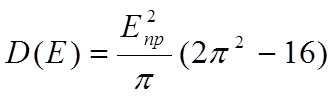 (1.7)
(1.7)
На интервале вероятностей от 0,01 до 0,99 интенсивность флуктуаций достигает 36 дБ.
Как показано в [ 2] ,число лучей больше 2, что связано с высокоэтажной застройкой, когда происходит затемнение основного луча. При уменьшении подвеса передающей антенны до уровня зданий, уменьшение уровня прямого луча может достичь очень малых значений. Случай Епр = 0 характерен для сильной застройки и низкого (ниже уровня зданий) подвеса передающей антенны.
Плотность распределения вероятностей суммарной волны (Епр = 0) при условии, что отражение волны имеют одинаковые амплитуды Е1 и случайные фазы, в соответствии с (1.5).
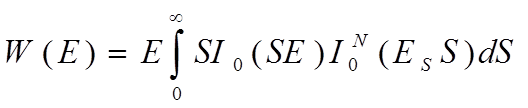 (1.8)
(1.8)
Решение (1.8) согласно (Головин Э.С. Мультипликативные помехи в сетях железнодорожной радиосвязи. – М: Радио и связь, 1985, 200 с.) приведет к следующему выражению:
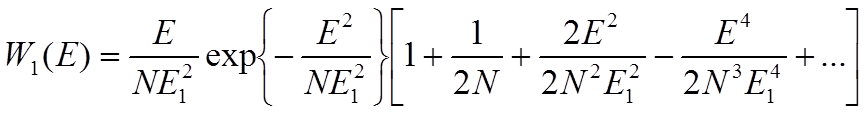 (1.9)
(1.9)
При N → ∞ выражение (1.9) переходит в плотность распределения Релея:
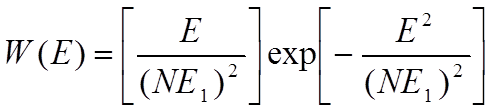 (1.10)
(1.10)
которому соответствует интегральная функция распределения
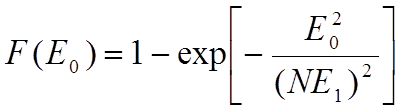 (1.11)
(1.11)
Интересно отметить, что при N = 4 выражение (1.9) практически переходит в (1.10).
Для этого случая
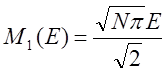 ;
; 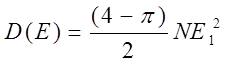
Диапазон флуктуаций для (1.10) по сравнению с (1.5) на уровне вероятностей от 0,01 до 0,99 достигает 26 дБ.
Если на трассе Епр ≠ 0, W11(ν) = δ(ν1 – Епр.), то согласно (1.3)
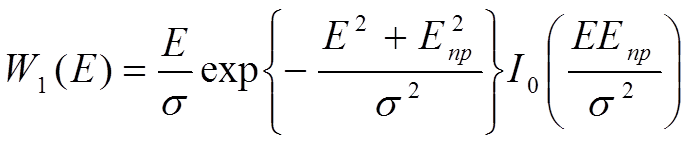 (1.12)
(1.12)
где σ = NE1
I0(x) – функция Бесселя нулевого порядка
Обозначив
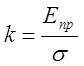 , то можно утверждать, что при изменении k
от 0 до k>>
1 диапазон флуктуаций Е изменяется от 26 дБ до 0 дБ.
, то можно утверждать, что при изменении k
от 0 до k>>
1 диапазон флуктуаций Е изменяется от 26 дБ до 0 дБ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.