Пусть при
автовыборе αm в
( 4.8) является индикатором канала, для которого отношение уровня несущей к
уровню шума удовлетворяет условию 
, тогда
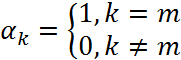
Представим принимаемый сигнал в k-ветви:
тогда плотность
вероятностей огибающей 
является рэлевской с мощностью 
, т.е.
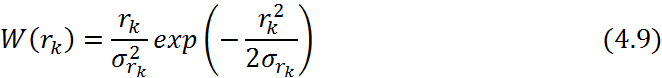
Отношение несущая/шум определяется, как:
Где 
-мгновенное значение квадрата огибающей сигнала в k-ой
ветви разнесения; 2 Nk –средняя
мощность комплексной огибающей nk(t) аддитивного шума в k-ой ветви
разнесения.
Известно, что
Тогда Гк есть отношение средней мощности сигнала к мощности шума в ветви разнесения
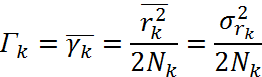
и, следовательно, выражение (4.9) приводится к виду
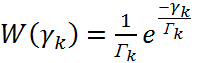(4.11)
Вероятность того,
что отношение несущая-шум в одном канале не превышает заданный уровень Х:
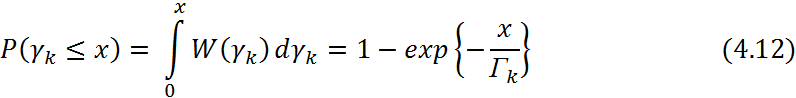
Вероятность того, что результирующее отношение несущая-шум не превысит Х, равно вероятности того, что γk во всех М ветвях разнесения одновременно не превысит уровня Х:
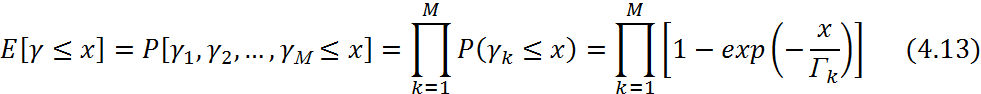
Целесообразность
применения автовыбора и порядка разнесения(число ветвей разнесения)
определяется в первую очередь характеристиками многолучевого порядка, точнее,
соотношением между 
Рассмотрим несколько примеров.
Пример 1.
Допустим, что все 
равны Г, т.е. средние значения отношения несущая-шум
на интервале времени, охватывающем быстрые замирания, равны для всех ветвей
разнесения, тогда
Характеристики сигнала улучшаются с увеличением числа ветвей разнесения, но темпы этого улучшения замедляются. Наиболее значительное улучшение происходит при переходе от одной к двум ветвям разнесения (рис.4.7).
Пример 2.
k=1,…,M
Так как в этом случае справедливо приближение
,
то выражение 4.13 принимает вид:
Пример 3.
В этом случае отношение несущая-шум γ оказывается существенно ниже среднего значения отношения несущая-шум в остальных М-1 ветвях разнесения, и выражение (4.13) принимает вид
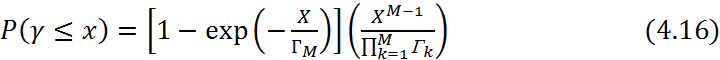
а при ГM<<x выражение (4.16) принимает вид:
Сравнение (4.17) и (4.15) подтверждает, что существенный вклад в результирующий сигнал вносят только(M-N) ветвей разнесения, где N-число ветвей разнесения, в котором среднее значение отношения несущая-шум оказывается существенно ниже заданного уровня (Г<<x) т.е.
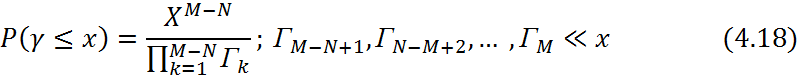
Пример 4.
Коррелированные сигналы.
В [19] определена совместная плотность вероятностей W(γ1,γ2) при коэффициенте корреляции р, которая имеет вид
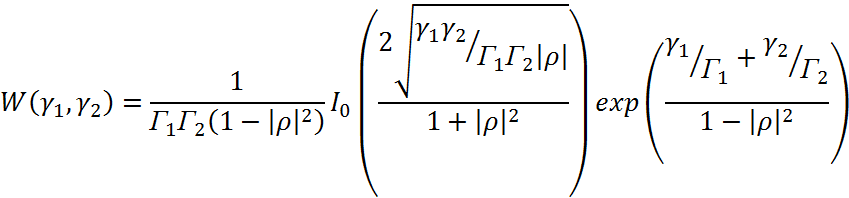
где
Полагая Г1=Г2 и подставляя (4.19) в (4.20)
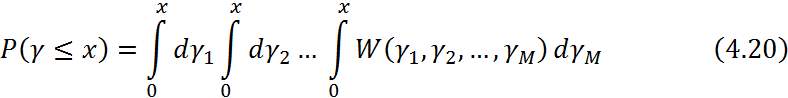
получаем
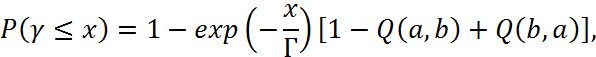
где
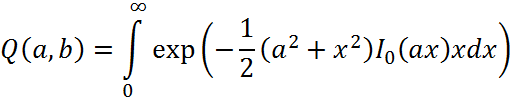
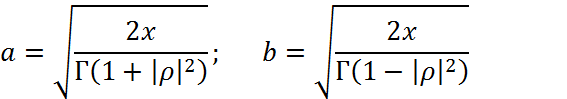
Для случая, когда X<<Г
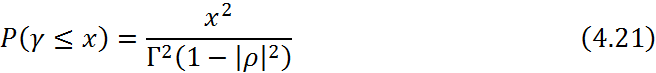
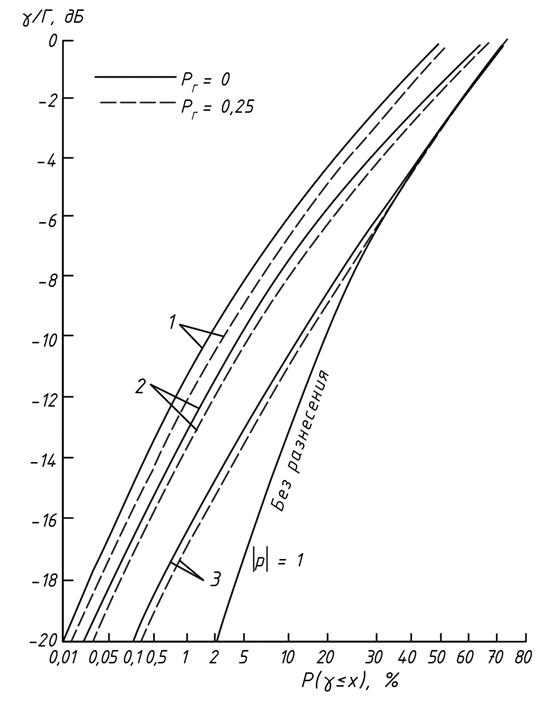
Рис. 4.7. Интегральная функция распределения вероятностей
при селективном комбинировании сигналов в ветвях
разнесения с равными мощностями сигналов:
1 - 
= 
; 2 - = 2 ; 3 - = 10
4.4. Комбинирование с коммутацией ветвей разнесения
Автовыбор ветвей разнесения трудно реализовать практически, поскольку при этом требуется использовать плавающий пороговый уровень. Поэтому комбинирование с переключением ветвей разнесения, использующее фиксированный пороговый уровень, представляется более реальной и практически осуществимой альтернативой комбинирования.
При комбинировании с коммутацией ветвей разнесения предполагаем, что два независимых сигнала r1(t) и r2(t), распределенных по закону Рэля, принимаются по двум ветвям разнесения, результирующую огибающую сигнала r(t) можно получить, используя стратегию коммутации и ожидания.
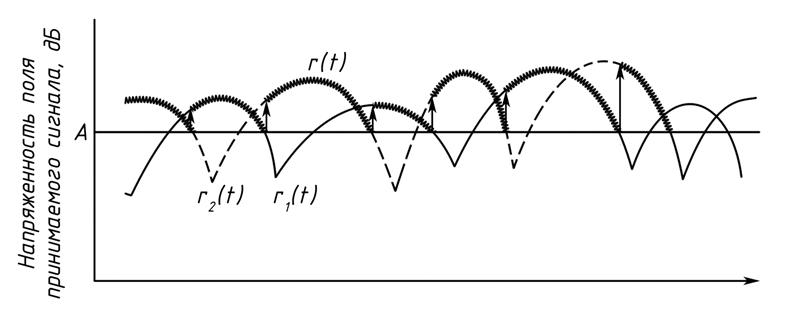
Рис.4.8. Комбинирование сигналов методом коммутации
ветвей разнесения
Стратегия заключается в выборе огибающей сигнала r1(t) или r2(t), ожидание момента, когда она окажется ниже заранее выбранного уровня А порога коммутации, и последующем переходе к ветви разнесения с более высоким уровнем сигнала (рис.4.8).
Вероятные характеристики метода комбинирования с коммутацией ветвей разнесения:
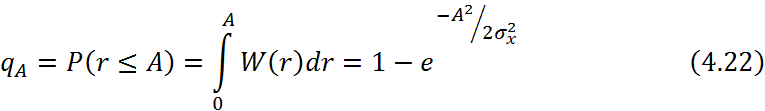
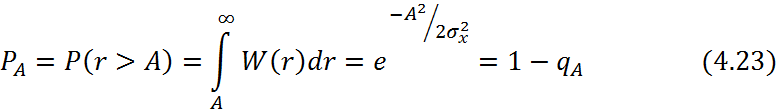
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.