Общий характер городского радиоканала. Системные функции для каналов со случайно изменяющимися параметрами. Особенности городского канала радиосвязи. Современные методы повышения помехоустойчивости цифровых сигналов в городских радиоканалах, страница 18

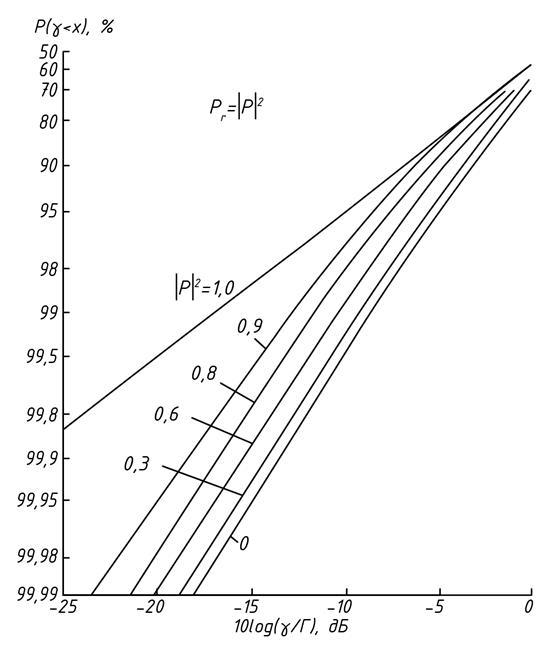
       Рис.4.10. Характеристики  комбинирования  сигналов в двух  коррелированных  ветвях  разнесения  методом  сложения, максимизирующего отношение сигнал-шум

      4.6.  Сложение  с равными  весами

        Метод додетекторного сложения, максимизирующий отношение сигнал/шум, является идеальным линейным методом разнесенного приема, однако реализация в приемнике оптимальных весовых коэффициентов не всегда возможны.

При автовыборе в любой момент времени выбирается ветвь разнесения с наиболее сильным сигналом, но это зачастую также трудно реализовать. Разнесенный прием с коммутацией ветвей разнесения всегда обеспечивает худшие характеристики  принимаемого сигнала по сравнению с автовыбором ветвей разнесения. По сравнению с этими методами при сражении с равными весами для сложения сигналов различных ветвей разнесения используются простые схемы сложения на основе ФАПЧ.  Метод сложения с равными весами обеспечивает некогерентное сложение шумов и когерентное сложение сигналов различных ветвей разнесения и является одним из вариантов линейного сложения при разнесенном приеме.

Результирующее отношение сигнал/шум при сложении с равными весами

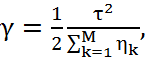                                                                                        (4.53)

где огибающая результирующего сигнала

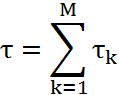
И  – огибающая сигнала в k-й ветви разнесена.

Плотность распределения вероятностей результирующего сигнала  может быть получена следующим образом:

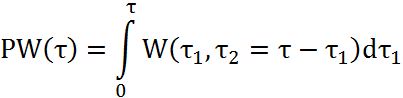
При малых значениях  в одной ветви разнесения – среднего значения несущая/шум в схеме сложения с равными весами, может быть использован метод, который усиливает связь этой величины с аналогичной величиной для схемы сложения, максимизирующей отношение сигнал/шум. При выполнении этого условия может быть использовано [19 ]

где

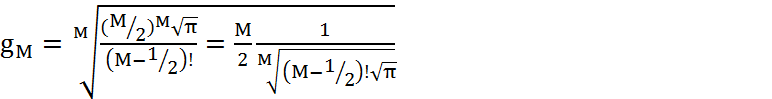(4.54)

Подстановкой (4.54) в (4.38) получим выражения для M=2,3,4

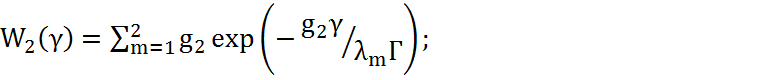(4.55)

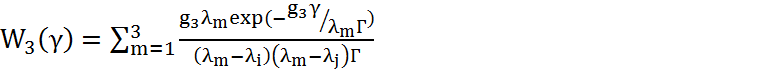(4.56)

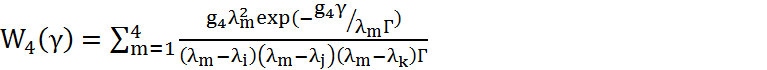(4.57)

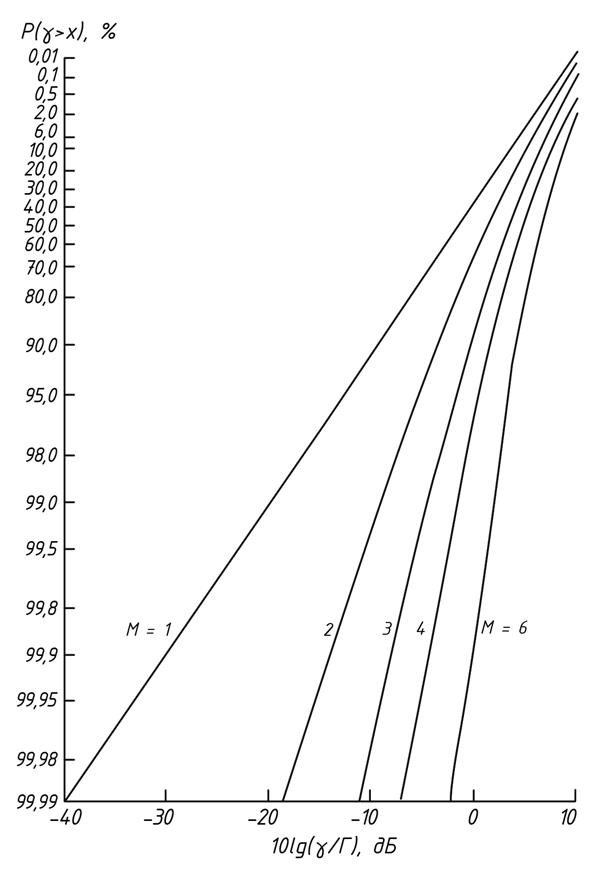
                       Рис.4.11  Интегральная  функция  распределения  вероятностей

                                        при  комбинированиисигналов  методом  сложения с

                                         с  равными  весами

       Исследование выражений (4.55)-(4.57) при различных 𝜸 дает несущественные погрешности по отношению к точным решениям.

Интегрируя (4.55) – (4.57) по 𝜸 в пределах от 0 до X можно определить функцию распределения вероятностей для различного числа ветвей разнесения.

     На  рис.4.11   приведена интегральная  функция  распределения  вероятностей  при  комбинировании  сигналов  методом  сложения  с  равными  весами  для  различного  числа  ветвей  разнесеня. Как  видно  из  рисунка  увеличение   количества   ветвей  более  3  нецелесообразно.

Сравнивая характеристики разнесенного приема при сложении с равными весами и сложения, максимизирующего отношение согнал – шум, можно установить, что сложение с равными весами имеет несколько худшие характеристики.

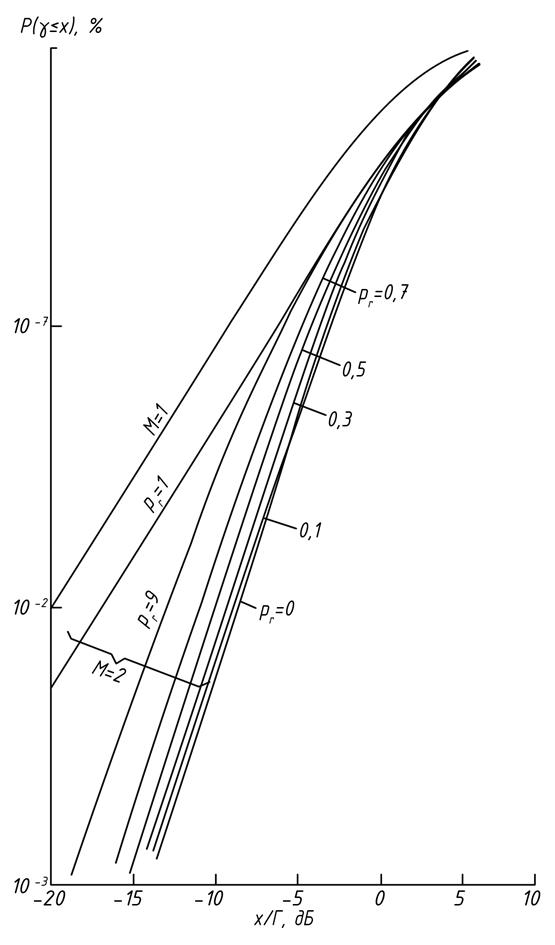
               Рис.4.12.Интегральная  функция  распределения   вероятностей  при

                               комбинировании  сигналов  в  двух  ветвях   разнесения

                               методом   сложения   с  равными  весами

Для нахождения функции распределения вероятностей двух коррелированных сигналов в схеме сложения с равными весами обозначим меру - коэффициент корреляции двух огибающих с релеевским законом распределения. Тогда приближенное выражение для функции распределения можно получить из (4.52)

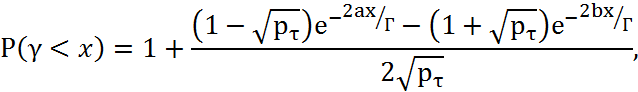
где ;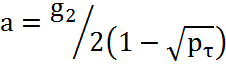

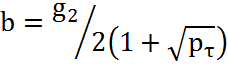
Из выражения (4.54) следует

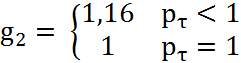
     На  рис.4.12  приведены   характеристики  разнесенного  приема  для  коррелированных  сигналов  в  ветвях  разнесения.  Как  видно  из рассмотрения,

увеличение  коэффициента   корреляции  с  0,5  до 1,0  сильно  снижает   эффектив-

ность  системы  с  разнесенем,  но  даже  при  полной  корреляции  сигналов  достигается   небольшой , но  выигрыш.

     5. Пространственно – временное  кодирование  дискретных  сигналов.