Общий характер городского радиоканала. Системные функции для каналов со случайно изменяющимися параметрами. Особенности городского канала радиосвязи. Современные методы повышения помехоустойчивости цифровых сигналов в городских радиоканалах, страница 11

                 На рис. 3.16 и 3.17 представлены графики распределения временных задержек и соответствующие им корреляционные функции частоты. Представленные выше зависимости характеристик для высокоподнятой передающей системы (выше уровня крыш) и низкоподнятой приемной системы (ниже уровня крыш).

               Нормированные корреляционные функции Р₁,Р₂,Р₃, вычисленные для распределения временных задержек, определяемых соответственно выражениями  (3.15, 3.16, 3.17) равны:

Р₁(∆f)=e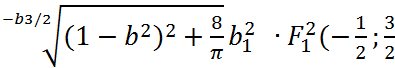 ;;                                                 (3.18)

P₂(∆f)=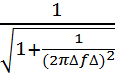                                                                                                   (3.19)

P₃(∆f)=Ι cos(2π∆f∆)Ι                                                                                              (3.20)

                  где  b=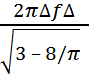и  F1 – вырожденная гипергеометрическая функция, которая определяется через модлорицированую функцию Бесселя первого рода:

                    ₁F₁(ν +; 2ν +1; Z) = 2^2ν Г(ν+1)Z^-νe^Z/2 I_ν()

                    Для случая низкоподнятых антенн заслуживают внимание следующие функции рассеяния:

1.  Нормальное распределение:

Р(τ) = σ²  ехр{ },                                                                         (3.21)

B_кор =  

(τ/4∆) для любых τ, τ>0, τ≤0, для которой корреляционная функция

K(∆f) = 2σ² exp { -4∆f²/B²_кор}                                               (3.22)

2.  Двустороннее  экспотенциальное распределение 

Р(τ) =,

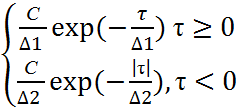         Глава 4. Современные методы повышения помехоустойчивости цифровых сигналов в городских радиоканалах

          4.1. Методы разнесения

  Метод разнесения используется для выделения информации из нескольких сигналов, передаваемых по независимо замирающим путям. Идея метода состоит в том, чтобы скомбинировать несколько сигналов и ослабить влияние чрезвычайно глубоких замираний [21-23].  Методы комбинирования сигналов требуют отдельного рассмотрения, поэтому будут рассмотрены ниже. Методы разнесения позволяют ослабить влияние замираний, поскольку глубокие замирания редко наблюдаются одновременно в течение одного и того же интервала времени для двух и более путей распространения.

  На рис 4.1. изображены два некоррелированных замирающих сигнала, принимаемых по независимо замирающим путям распространения.

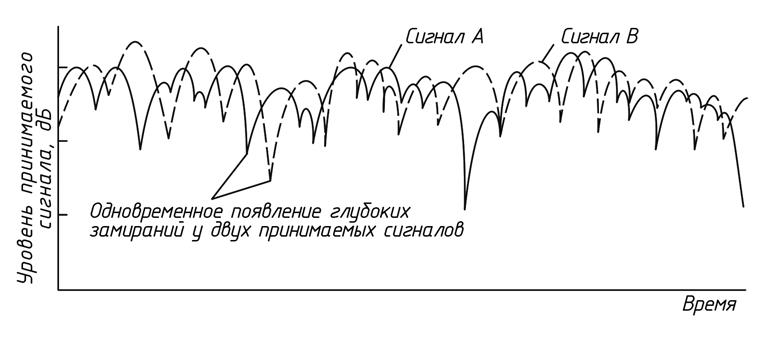
               Рис.4.1. Некоррелированный  сигналы  принимаемые  на  антенны ,

                             разнесенные  в  пространстве

  Поскольку вероятность возникновения двух глубоких замираний для двух некоррелированных сигналов в некоторый момент времени невелика то влияние замираний может быть ослаблено путем соответствующего комбинирования сигналов.

  В существующих методах разнесения могут быть выделены три обобщенных класса:

Первый класс ( метод макроскопического разнесения )- это разнесение, которое используется для комбинирования двух и большего числа медленно замирающих сигналов с логнормальным законом распределения, которые соответствуют независимо замирающим путям распространения, формируемым с помощью двух или большего числа антенн, расположенных на различных базовых станциях, разнесенных в пространстве.

Метод макроскопического разнесения позволяет устранить влияние затенения зон приема и другие явления, связанные с шероховатостью рельефа, путем передачи и приема сигналов базовых станций, расположены в двух различных, разнесенных в пространстве, точках.(Много базовые разнесения)

Второй класс (метод микроскопического разнесения) – это разнесение, которое используются для разнесения комбинирования двух или большего числа быстро замирающих сигналов с Рэлевским законом распределения, которые соответствуют независимо замирающим путям распространения, формируемым двумя или большим числом разнесенных антенн, расположенных на одной и той же приемной станции.