Например, наряду с прямым преобразованием Фурье, определяемым (2.1 – 2.3), справедлива также формула
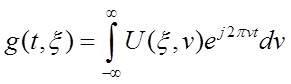 (2.4)
(2.4)
и т.д.
Нетрудно видеть, что
между сигналом ![]() (или его спектром
(или его спектром ![]() ) на входе канала и сигналом
) на входе канала и сигналом ![]() (или его спектром
(или его спектром ![]() )
на выходе канала существуют следующие соотношения:
)
на выходе канала существуют следующие соотношения:
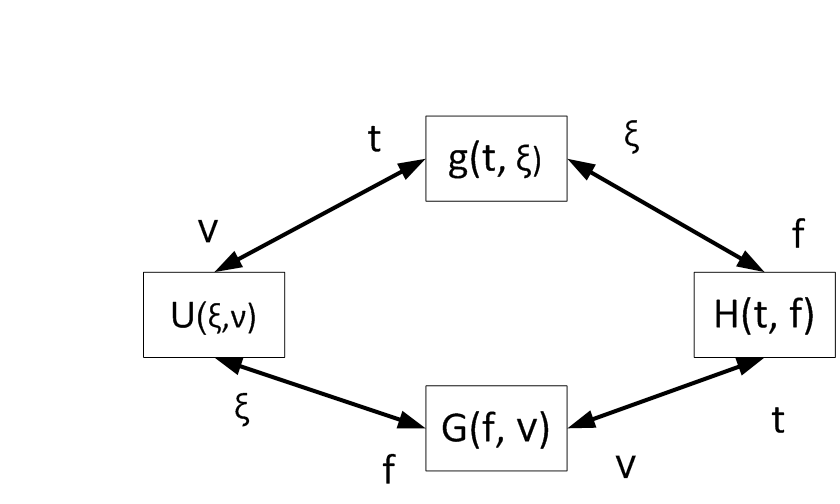
Рис 2.1
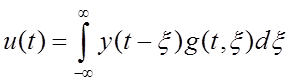 (2.5)
(2.5)
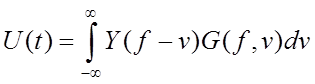 (2.6)
(2.6)
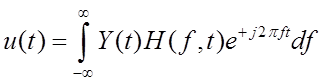 (2.7)
(2.7)
Используя формулы (2.7) и (2.4), имеем
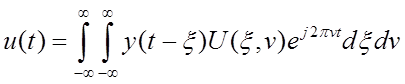 .
.
Системные функции ![]() ,
, ![]() ,
, ![]() ,
, ![]() большинства
реальных каналов с переменными параметрами следует рассматривать как случайные.
Физически это отражает наличие замираний. Принято различать общие и селективные
замирания. Общие замирания имеют место, если ширина полосы частот
большинства
реальных каналов с переменными параметрами следует рассматривать как случайные.
Физически это отражает наличие замираний. Принято различать общие и селективные
замирания. Общие замирания имеют место, если ширина полосы частот ![]() сигнала существенно меньше интервала
корреляции
сигнала существенно меньше интервала
корреляции ![]() передаточной функции
передаточной функции ![]() канала по частоте, а длительность
канала по частоте, а длительность ![]() , причем
, причем ![]() –
интервал корреляции функции
–
интервал корреляции функции ![]() по времени. Если
условие
по времени. Если
условие ![]() не выполняется, имеют место
частотно-селективные замирания, а при невыполнении условия
не выполняется, имеют место
частотно-селективные замирания, а при невыполнении условия ![]() – временные селективные замирания. При
одновременном невыполнении условий
– временные селективные замирания. При
одновременном невыполнении условий ![]() и
и ![]() имеют место временные и
частотно-селективные замирания. В зависимости от величины отношений
имеют место временные и
частотно-селективные замирания. В зависимости от величины отношений ![]() и
и ![]() можно
различать медленные
можно
различать медленные 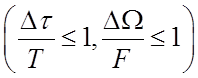 и быстрые
и быстрые 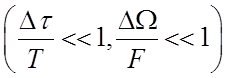 селективные замирания.
селективные замирания.
Условие ![]() позволяет представить данную модель
линейной системой с постоянными параметрами. Существование замираний отражается
наличием совокупности реализаций случайной функции
позволяет представить данную модель
линейной системой с постоянными параметрами. Существование замираний отражается
наличием совокупности реализаций случайной функции ![]() .
.
Системные функции для данной модели имеют вид:
![]()
![]()
Используя выражения 2.1 и 2.3, находим, что
![]()
![]()
Следовательно, для
описания данного канала достаточно использовать две функции ![]() и
и ![]() , причем
они связаны между собой преобразованиями Фурье.
, причем
они связаны между собой преобразованиями Фурье.
Связь между сигналами на
входе ![]() и выходе
и выходе ![]() канала,
их спектрами
канала,
их спектрами ![]() и
и ![]() и
системными функциями описывается формулами:
и
системными функциями описывается формулами:
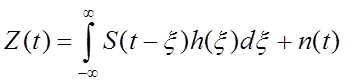
![]() (2.8)
(2.8)
Для статистического описания системных функций удобно использовать математическое ожидание, описывающее регулярную составляющую замираний
![]()
![]()
и корреляционные функции
![]()
![]()
Функция корреляции ![]() дает меру корреляции замираний случайной
составляющей импульсного отклика. В частности, когда
дает меру корреляции замираний случайной
составляющей импульсного отклика. В частности, когда
![]() ,
(2.9)
,
(2.9)
где 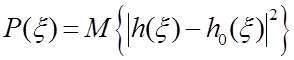 –
распределение мощности случайной компоненты импульсного отклика
–
распределение мощности случайной компоненты импульсного отклика ![]() , пути распространения с разными временными
сдвигами будут не коррелированны.
, пути распространения с разными временными
сдвигами будут не коррелированны.
Функция ![]() дает меру частотной селективности
замираний. Сущность частотно-селективных замираний удобно проиллюстрировать
следующим образом. Подадим на вход канала два комплексных моночастотных сигнала
дает меру частотной селективности
замираний. Сущность частотно-селективных замираний удобно проиллюстрировать
следующим образом. Подадим на вход канала два комплексных моночастотных сигнала
![]() и
и ![]() . На
выходе канала имеем сигналы
. На
выходе канала имеем сигналы ![]() и
и ![]() . Мерой корреляции мгновенных значений
комплексных амплитуд этих сигналов является значение функции корреляции
. Мерой корреляции мгновенных значений
комплексных амплитуд этих сигналов является значение функции корреляции ![]() . Если величина этой функции близка к единице,
то говорят, что на данных частотах имеют место общие или плоские замирания. В
противном случае замирания считают частотно-селективными.
. Если величина этой функции близка к единице,
то говорят, что на данных частотах имеют место общие или плоские замирания. В
противном случае замирания считают частотно-селективными.
Связь между функциями
![]() и
и ![]() можно
установить, учитывая, что
можно
установить, учитывая, что ![]() . Тогда
. Тогда
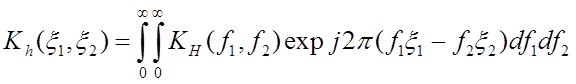 (2.10)
(2.10)
Соответственно, справедливо двумерное обратное преобразование Фурье.
По характеру функции ![]() можно различать каналы:
можно различать каналы:
– без регулярной
составляющей, когда ![]() ;
;
– с регулярной составляющей,
интенсивность которой не зависит от частоты, т.е. ![]() ; в
этом случае регулярная составляющая имеется только в одном луче, т.е.
; в
этом случае регулярная составляющая имеется только в одном луче, т.е. ![]() ;
;
– с регулярной составляющей, интенсивность которой зависит от частоты; регулярная составляющая в этом случае имеется больше, чем в одном пути распространения.
В каналах без регулярной составляющей действует механизм рассеяния, поэтому замирания носят часто случайный характер.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.