Итак, мы рассмотрели вероятностные модели радиоканала [3], которые не в полной мере описывают характер поля в городе. Но эти модели более пригодны для расчета помехоустойчивости цифровых подвижных систем связи.
Порядок обоснования модели канала складывается из следующей последовательности анализа
- задание высот подвеса передающей и приемной антенн.
- квалификация застройки зоны обслуживания систем связи
- рассмотрение структурной многолучевости, которая включает в себя количество лучей N и характер импульсной реакции канала
- выбора набора моделей, так как уровень сигнала притерпивает очень сильные изменения даже внутри небольших зон обслуживания.
Для задач анализа помехоустойчивых цифровых систем только с гладкими замираниями рассмотренные модели очень приблизительны. Поэтому если анализ поля на этом заканчивается и модели не будут использованы в дальнейшем, то есть возможность усложнить модель и сделать ее более адекватной, учесть более тонкую структуру поля.
В [4 ] приведено вероятностное описание амплитуд сигналов в системах подвижной связи. Характерной особенностью такого канала передачи при движении подвижного объекта (ПО) являются флуктуации амплитуды сигнала, содержащие три составляющие: быструю, определяемую интерференцией копий сигнала, пришедших в точку приема по многим путям; медленную, вызванную затемнение трассы распространения рельефом растительностно и местными предметами; очень медленную, соответствующую изменениям дальности связи и рефракционных свойств атмосферы. В этом случае статистические принятые модели флуктуаций амплитуды сигнала, например, законы Рэлея, Райса во многих случаях неадекватны.
В работе [5] на основе экспериментальных данных предлагается следующая плотность распределения вероятностей:
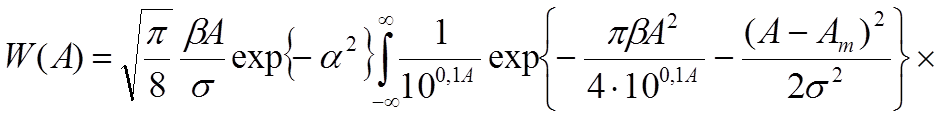
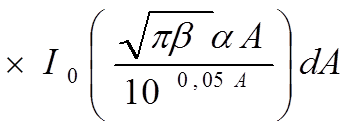(1.13)
где
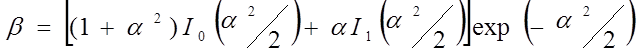
Аm – медленное значение локального среднего уровня амплитуды в пределах глобальной зоны перемещения ПО
σ – среднеквадратическое отклонение нормального закона флуктуаций локального среднего значения уровня сигнала в пределах глобальной зоны, определяемое на основе типа подстилающей поверхности
α2 – отношение локальных средних мощностей регулярной и случайных компонентов сигнала
I0(x) и I1(x) – моделированные функции Бесселя первого рода 0- и 1-го порядка соответственно.
Данная модель универсальна, она соответствует условиям функционирования систем мобильной связи в городских условиях, пригороде и на открытой местности.
Для статистического представления амплитуды сигналов систем мобильной спутниковой связи также используются сложные законы распределения вида:
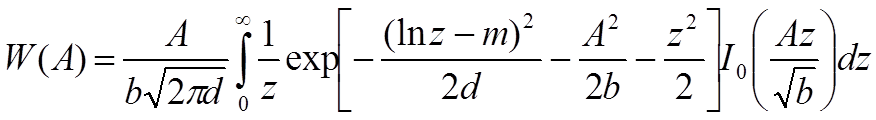
(1.14)
где b– средняя мощность переотраженного многолучевого сигнала (рассеянной составляющей)
m – среднее значение уровня огибающей сигнала
d– дисперсия огибающей при наличии затенения.
Такая модель удовлетворительно описывает огибающую сигнала, являющегося результатом взаимодействия прямого луча и многолучевой рассеянной компоненты.
Упрощение (13) и (14) с достаточно высокой точностью приводит к выражению следующего вида:
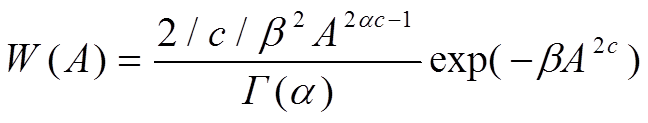(1.15)
где α > 0, с ≠ 0 – параметры формы;
β > 0 – параметр масштаба;
Г(z) – Гамма-функция
Достоинством
[6] является возможность получения путем вариации параметров α, с,
β известных законов распределения амплитуд радиосигналов Так, при α
= с = 1, β =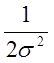 
(1.15) преобразуется в
закон Рэлея, при α = 0,5n, с = 0,5 и β =
0,05 в хи-квадрат распределения, при α = m, 
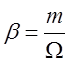и с = 1 – в закон Накагами, при с
= 0,5 в Гамма-распределение, при α = 1, с = 0,5ν – в закон
Вейбулла.
Плотность распределения вероятностей (1.15) позволяет также с высокой степенью точности аппроксимировать k-распределение, распределение Беккмана и Накагами-Райса . Предельным случаем распределения (1.15) при с → 0 является логарифмический нормальный закон, который также является предельным для (1.13), (1.14).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.