Общий характер городского радиоканала. Системные функции для каналов со случайно изменяющимися параметрами. Особенности городского канала радиосвязи. Современные методы повышения помехоустойчивости цифровых сигналов в городских радиоканалах, страница 16

где

В большинстве случаев коммутация осуществляется при достижении фиксированного порогового уровня А, как показано на рис. 4.8

Чтобы найти значение функции распределения для некоторого произвольного уровня В, воспользуемся выражением:

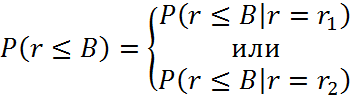
  Поскольку r₁ и r₂  статически неразличимы, то:

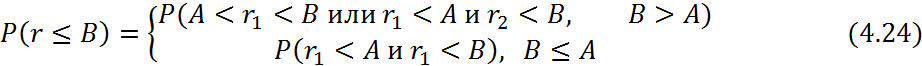
Где

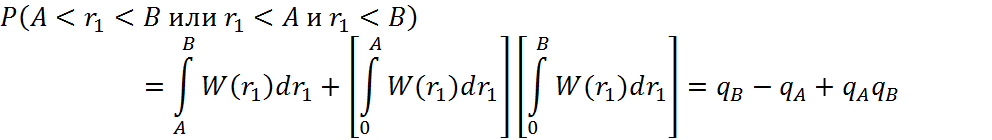
а q_A и q_B определяются в соответствии с (4.22)

Вероятность  P (r₁ < A и r₁ < B)  может быть представлена в виде:

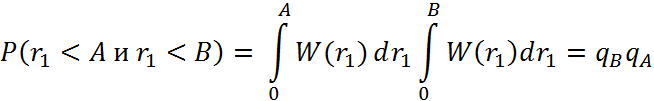
Следовательно, выражение (4.24) примет вид:

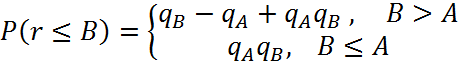
         Результаты комбинирования сигналов в двух ветвях разнесения методом автовыбора при различных значениях порогового уровня подробно рассмотрены в [19],  где  представлены функции распределения случайной величины для различных значений порога коммутации А.  Отсюда  следует, что улучшение характеристик сигнала наблюдается при условиях сигнала выше порогового.

При условиях ниже порогового сигнал подчиняется закону распределения Рэлея. Причем характеристики сигнала при комбинировании с коммутацией ветвей хуже характеристик сигнала, получаемого при автовыборе, за исключением случая, когда уровни равны пороговым. В этом случае они эквивалентны.

     4.5.   Сложение, максимизирующее  отношение  сигнал – шум

При сложении, максимизирующее отношение сигнал/шум, осуществляется весовое сложение предварительно сфазированных М сигналов для получения оптимальных характеристик сигнала.  Как отмечено выше, при додетекторном сложении сигналы фазируются на промежуточной частоте.  Сложение, максимизирующее отношение, может быть реализовано и после детектора. После каждого детектора в этом случае необходимо включить регулировку усиления.

Комплексная огибающая сигнала для каждой ветви разнесения на входе изменного тракта П4 может быть представлено, как:

где a₀(t)– сигнал, изменяющийся во времени; u_k(t) – замирающий сигнал, вызванный многолучевым характером распространения, без зеркального компонента. В случае линейного додекторного сложения, комплексная огибающая выходного сигнала

                        
                                   (4.25)

                                                                                                                                                                   

Выражение для результирующего сигнала S(t) и шума n(t) имеют вид :

(4.26)

                                                                                                                                                                     

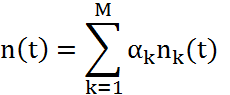
Без потери общности допустим, что     на интервале времени 2T и средней квадрата огибающей равно единице.

Отклонение несущая/шум:

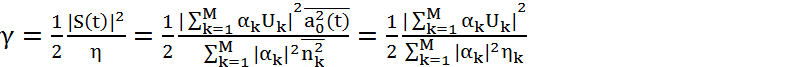(4.27)

                                                                                                                                                                      

Используя неравенство Шварца для комплексных чисел, можно получить:

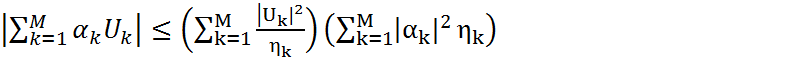(4.28)

Подставляя (4.28) в (4.27), получим:

(4.29)

                                                                                                                                                                Для получения максимума в выражении (4.29) необходимо в выражении (4.28) оставить только знак равенства. Знак равенства имеет место тогда и только тогда, когда

(4.30)

Для каждого значения k, где k – произвольное комплексное число.

Из (4.30) следует, что оптимальный весовой коэффициент для каждой ветви прямо пропорционален величине, копмлексно сопряженной с замирающим сигналом, и обратно пропорционален мощности шума в ветви разнесения.

Выражение (4.29) может быть переписано для максимального отношения несущая/шум на выходе следующим образом:

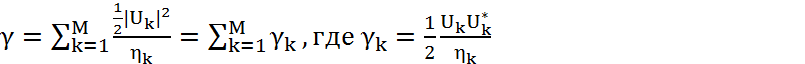(4.31)

Случайная величина (4.31) подчиняется закону распределения χ².

Для вычисления плотности распределения вероятностей, положим что каждая из М соответственно распределяемых комплексных гауссовских величин определяется, как:

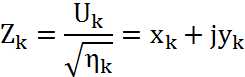
Тога плотность распределения вероятностей М пар действительных гауссовских величин

(4.32)

Где [Z] – столбец матрицы с элементами  ; [⋀] – ковариационная матрица размером М х М, которая выражается в виде:

(4.33)