Общий характер городского радиоканала. Системные функции для каналов со случайно изменяющимися параметрами. Особенности городского канала радиосвязи. Современные методы повышения помехоустойчивости цифровых сигналов в городских радиоканалах, страница 26

Случайная величина q на входе решающего устройства на рисунке 4.1 может быть представлена как

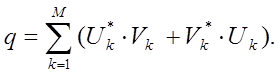
Вероятность ошибки  и  определяется как [10]

	(6.4)
	(6.5)

где M - число ветвей.

Отношение сигнал/шум , определяется как

(6.6)

где  , , , .

Момент  определяется как

(6.7)

где

	(6.8)

Если представить

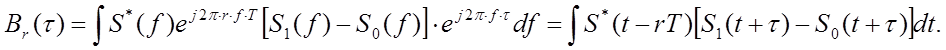
Таким образом, выражение (4.8) можно привести к

(6.9)

Учитывая, как показано в [22], частотно-корреляционная функция имеет Гауссовский характер:

(6.10)

где - полоса когерентности (или интервал корреляции), определяется на уровне 1/е,  -  средняя мощность сигнала.

Функция расширения задержек, соответствующей (4.10)

(6.11)

Частотно-корреляционная функция (4.10) для разных городов и различных высот подвеса антенн имеет различный вид [2] и отличается полосой когерентностью . Гауссовский характер функции выбран из расчета, что она соответствует наихудшим условиям распространения, при этом подвесы как передающей так и приемных антенн находятся значительно ниже уровня зданий, что соответствует полному затенению объектов.

Дальнейшие расчеты будем проводить для 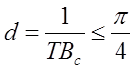, что соответствует попаданию 99,5% всей рассеянной мощности в интервал задержек .

Таким образом при анализе влияния межсимвольной интерференции (МСИ) обычно учитываются только импульсы примыкающим к интервалу , поскольку частотно-селективные замирания предполагаются слабовыраженными.

Вероятность  того, что зарегистрирована 1 при передаче 0 при наличии МСИ

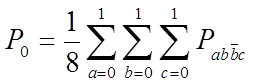,  где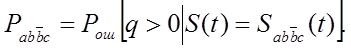 

Здесь - сегмент , соответствующий передаче последо-вательности символов , в предположении, что в отсутствии селективных замираний на интервале  фактически принимается последовательность .  Величина b, т.е  и .

Вероятность того, что вследствие МСИ будет зарегистрирован символ 0 при условии, что при передаче отсутствовали переходы сигналов, определяется как

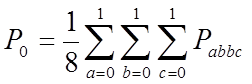,  где

Здесь интерпретируется аналогично .

Расчет помехоустойчивости начнем с определения сигналов ДОФМ

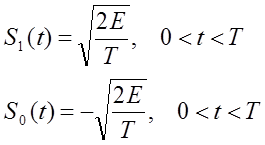
Для определения эквивалентного отношения сигнал/шум  (6.6) необходимо определить моменты . Для определения моментов воспользуемся выражением (4.7)

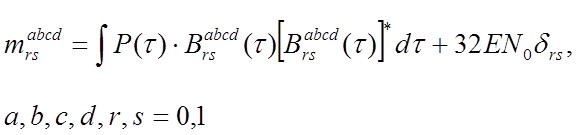
Функции корреляции определяется как

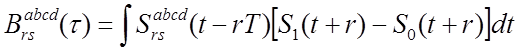
Приведем некоторые функции опуская остальные

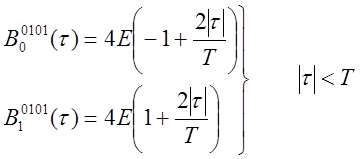
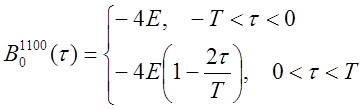
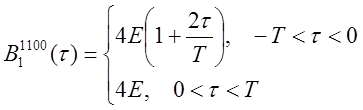
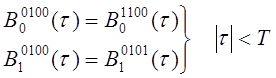
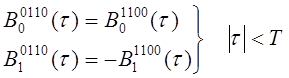
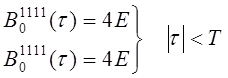
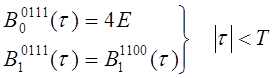
Подставляя рассчитанные значения моментов в формулу (6.6), получаем

	(6.14)
	( 6.15)
	(6.16)
	(6.17)
	(6.18)
	(6.19)

Учитывая все выше изложенное, определим вероятность ошибки как

(6.20)

где

	(6.21)
	(6.22)

Выражения (6.21) и (6.22) сокращены с учетом

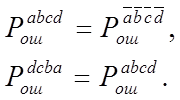
Оператор  представляет собой выражение (6.4) или (6.5)

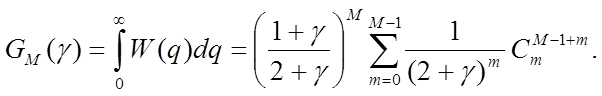
Для определения вероятности неустранимой ошибки, в выражении (6.15, 6.16, 6.17, 6.19) необходимо поставить  и найти предел.

Таким образом

	(6.23)
	(6.24)
	(6.25)
	(4.26)

Вероятность ошибочного приема 0 и 1

	(6.27)
	(6.28)

Средняя вероятность неустранимой ошибки определяется как

(6.29)

На рисунке 6.2 показана зависимость  для различных М.

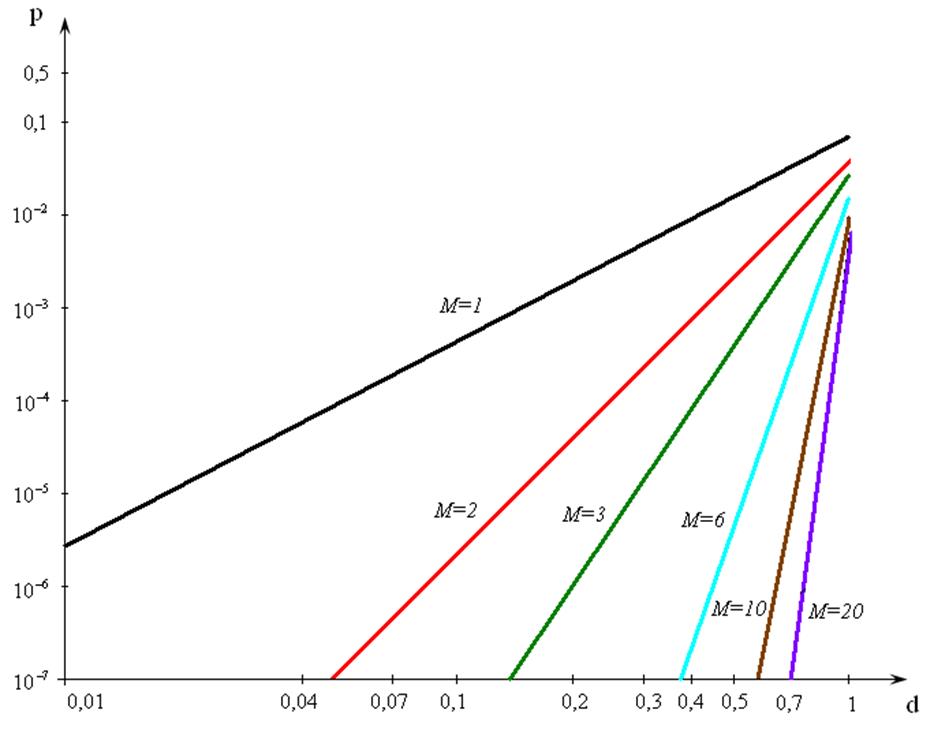
Рисунок 6.2 – Зависимость вероятности ошибки от полосы когерентности канала

6.2  Помехоустойчивость  разнесенного  приема  с  использованием

        пространственно – временного  кодирования

Как было показана в 5-ой главе данной работы метод Аламоути позволяет за счет использования двух передающих и M – приемных антенн получить порядок разнесения 2M. Разнесение на передаче требует излучение в половину мощности, чтобы общая мощность излучения не была увеличена. По сравнению с разнесением на приеме, уменьшение отношения сигнал/шум составляет 3дБ. С другой стороны уменьшение излучающей мощности на передаче благоприятно сказывается на требованиях к линейности усилителей и его стоимости. Недостатком метода Аламоути является использование количества передающих антенн кратных  , где n – целые числа. То есть количество эффективно используемых антенн равно соответственно 2, 4, 8, 16 и т.д. Существуют коды и для 3-х антенн, но они малоэффективны.