Общий характер городского радиоканала. Системные функции для каналов со случайно изменяющимися параметрами. Особенности городского канала радиосвязи. Современные методы повышения помехоустойчивости цифровых сигналов в городских радиоканалах, страница 10

200 кГц  до 800 кГц при изменении частоты f₀  от 100 МГц  до 600 МГц,  при

этом связь линейная.

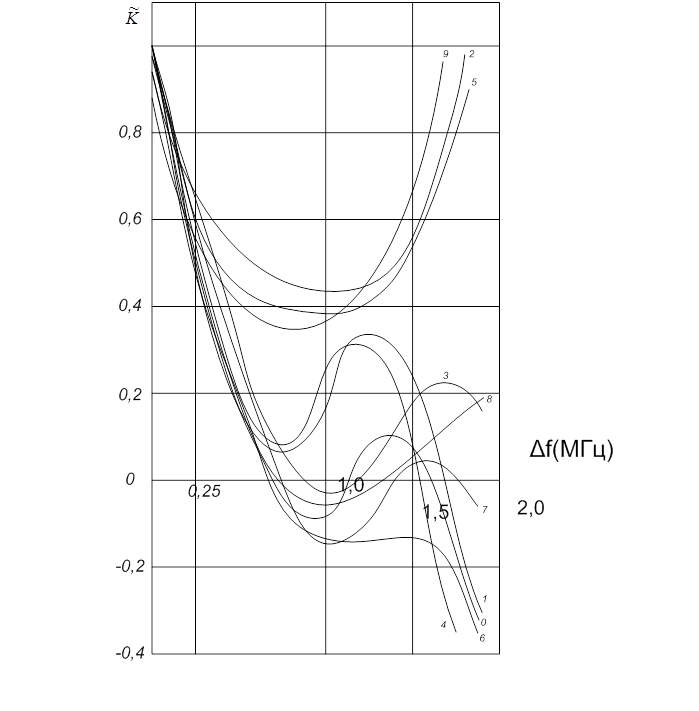
                      Рис.3.16  График  функции  корреляции  от  частотного  разнесения

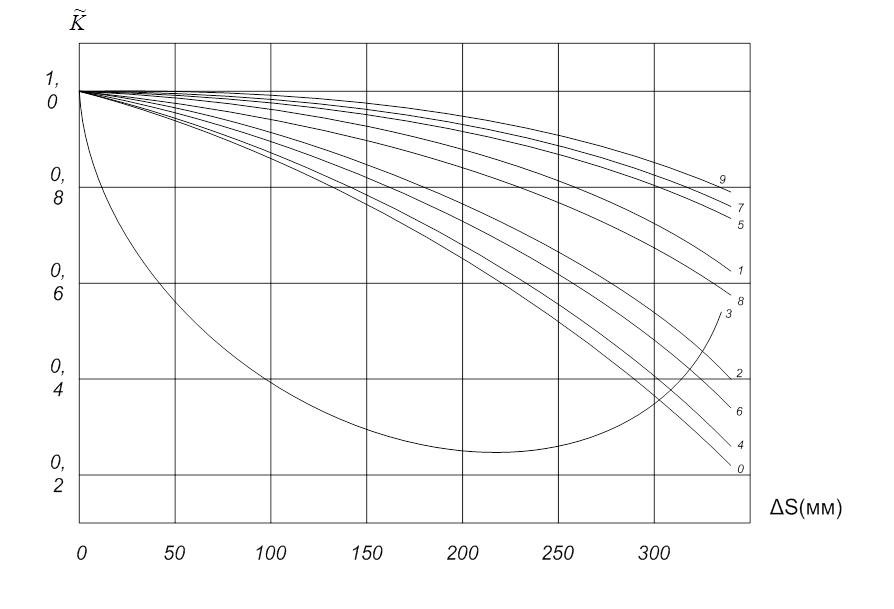
            Рис.3.17  График  функции  корреляции  от пространственного разнесения

                 Результаты экспериментальных исследований характеристик

многолучевости  метровых волн подробно изложены в [15], где измерение

производилось для условий подвеса передающей антенны, равной 290 м

(передающая антенна телевизионного вещания  г.Санкт-Петербурга),  а

приемная – 4м, установленной на автомобиле.

                   На рис. 3.10 и 3.12 представлены зависимости относительной

интенсивности отроженных лучей от времени задержки относительно

регулярного прямого  луча на вертикальный штырь   и   горизонтальный

диполь  (λ/2)  в  городе.

              Хотя излучаемый сигнал имеет горизонтальную поляризацию и

горизонтальный диполь очень слабо-выраженную диаграмму

направленности, диапазон отроженных лучей при приеме на вертикальный

штырь значительно больше, нежели на горизонтальный диполь.

              Как показали экспериментальные исследования функция рассеяния

Р(τ) может быть аппроксимирована как:

                         Р(τ)= С/∆ exp {-τ/∆},   τ0                             (3.10)

где Δ – среднеквадратическое отклонение, характеризующее степень

застройки районов города.

               Первая зона – прямая видимость основного луча, характеризуется,

как правило, однолучевым распространением; вторая зона – слабое

затемнение основного луча, число лучей равно 2-3; третья зона – сильное

ослабление прямого луча, число лучей 3-4 и более. При всех измерениях

основной луч присутствовал всегда, что говорит о регулярной составляющей

импульсного отклика канала.

                  Сопоставляя экспериментальные исследования [15-16] и теоретические

[18-21] рассмотрим несколько моделей Р(τ) и К(Δf) имеющих практическое

значение.

                  Как показано выше изменение коэффициента передачи i-волны может быть определено выражением:

                                  Е ⁱ_z = _i exp{j(ω_C - βVcos_i)(t - ∆t) - jω_CT_i}                             (3.11)

где βVcosφ_i – допплеровский сдвиг; ∆t – временной сдвиг, обусловленный движением объекта; β=2π/λ, λ – длина волны; Т_i – временная задержка i-ой волны.

            Результирующий сигнал определяется суммированием всех волн:

                            S(t) = _i exp{-j(ω_C - βVcos_i)(t – Δt - jω_CT_i)}                        (3.12)

         C увеличением t  фаза сигнала изменятеся пропорционально βVtcosφ_i, поэтому корреляционная функция аргумента ∆t = t₁ – t₂ определяется спектром допплеровских частот S(f):

                                         (∆t) = ^ej2πfc∆tdf                                                   (3.13)

           При изменении излучаемой частоты f_C  фаза каждой волны изменяется от значения Т_i, поэтому корреляционная функция аргумента ∆f = f₁ – f₂  определяется характеристиками распределения задержки Р(τ), которая связана с частотой корреляционной функцией следующим образом:

                           (∆f)=exp{j2π∆fτ} dτ                                                       (3.14)

           Для описания распределения временных задержек Р(τ) могут быть использованы следующие модели:

1.  Модель распределения Максвела:

P₁(τ) =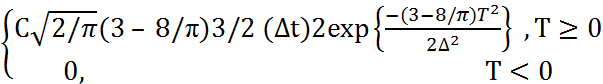                                    (3.15)

         где С – полная мощность, принимаемой антенной; Т – задержка, измеренная относительно прямого пути между базовой станцией и подвижным объектом;  ∆ - стандартное отклонение временных задержек;

2.  Модель экспотенциального распределения

                               Р₂(τ) = 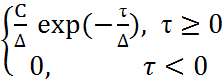                                                         (3.16)

3.  Аппроксимируюшая модель

                     P₂(τ) =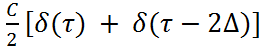                                                    (3.17)