Первая зона- прямая видимость основного луча, характеризуется, как правило, однолучевым распространением; вторая зона- слабое затенение основного луча, число лучей равно 2-3; третья зона- сильное ослабление прямого луча, число лучей 3-4 и более.
3.2 Функция рассеяния и частотная корреляционная функция городского канала связи
Методики определения средней вероятности ошибки в каналах с селективными замираниями построены таким образом,что основу расчетов составляет функция рассеяния по времени и частоте:
![]() (3.2)
(3.2)
где P(τ) характеризует меру рассеяния мощности сигнала по задержкам, P(f) – по доплеровским сдвигам частоты.
Кроме (3.2), удобно пользоваться функцией частотной корреляции канала:
![]() (3.3)
(3.3)
Замирающие сигналы могут иметь различные задержки, это может привести к возникновению коррекции между двумя сигналами, слабо разделенными по частоте.
Разнос частот, при котором корреляция зависит от расширения задержки Δ. Этот интервал частот получил название полосы когерентности или полосы корреляции – В корреляции.
Для иллюстрации явления расширения задержки обычно используют модель, в которой за импульсом, соответствующим приему сигнала, прошедшего по прямому пути, следуют импульсы, соответствующие рассеяным компонентам сигнала, амплитуда которых экспотенциально убывает. Предполагается, что первый импульс, в отличие от остальных, приходит на подвижный объект (ПО), не испытывая искажения по пути, без дисперсии. Затухающая часть сигнала формируется из большого числа компонентов, соответствующих различным лучам распространения, и, следовательно, имеет конечную полосу корреляции.
Нормированное выражение, представляющее преобразование Лапласа от огибающей в условиях расширения задержки, называется корреляционной функцией сигнала К(f). На рис. 3.8 представлены обощенные характеристики канала: импульсный отклик и корреляционная функция.
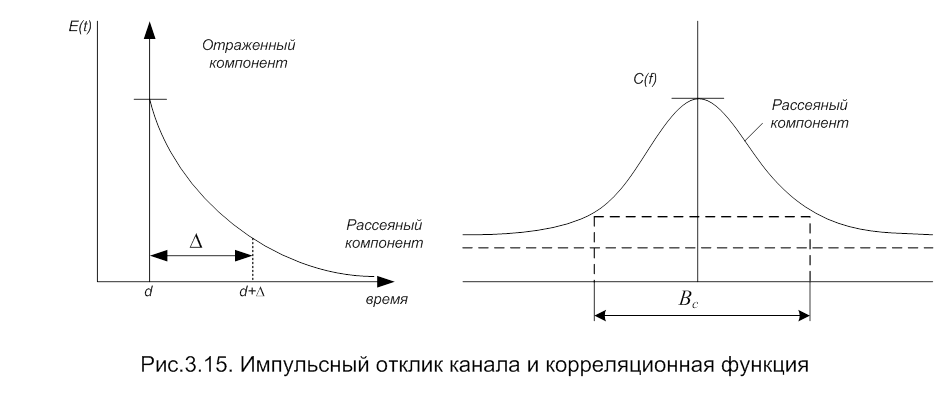
Как показано [15] полоса когерентности для трассы распространения длиной 2-4 км лежит в диапазоне 0,1 – 1 Мгц, изменяясь обратно пропорционально числу лучей, по которым происходит распространение.
Итак, полосой частотной когерентности канала мы определили максимальную ширину полосы частот, в пределах которой статистические свойства коэффициентов передачи двух гармонических сигналов жестко коррелированы.
Полосой частотной когерентности может быть также определено, как частотный разнос, для которого амплитуда нормированной корреляционной функции меньше некоторой величины А, где А всегда меньше 1.
Р(ΔfA) ≤ A,
где ΔfA = B кор. – полоса частотной когерентности.
Обычно, А пологают равной 0,5 для нормированной корреляционной функции огибающих, так и для нормированной корреляционной функции фаз.
В большинстве практических случаев:
Вкор.≈ 1/(8∆) (3.4)
В канале с частотно-селективными замираниями сигналы двух достаточно широко разнесенных частот будут замирать независимо. Это означает, что две частоты лежат в полосе частотной некогерентности. Следовательно, если одно и то же сообщение – речевое или дискретное – одновременно передается на нескольких частотах, то замирающие сигналы при приеме являются статически независимыми. Поскольку частотная селективность в значительной степени определяется диапазоном разброса задержек между отдельными компонентами многолучевых сигналов, то чем больше разброс временных задержек многолучевого сигнала, тем меньше полоса некогерентности двух гармонических сигналов.
Представим, что если принимаемый сигнал на ПО в виде:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.