Общий характер городского радиоканала. Системные функции для каналов со случайно изменяющимися параметрами. Особенности городского канала радиосвязи. Современные методы повышения помехоустойчивости цифровых сигналов в городских радиоканалах, страница 17

Где  и - комплексно – сопряженная и транспонированная матрица соответственно.

Тогда отношение несущая/шум на выходе:

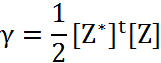
Характеристическая функция случайной величины

   (4.34)

Тогда плотность распределения вероятности может быть получена как обратная преобразовании Фурье:

(4.35)

В [19 ]было показано, что :

Ковариационная матрица [⋀], определяемая выражением (4.33), может быть записана в форме:

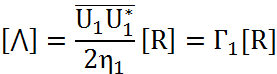
Где Г₁ – отношение несущая/шум в первой ветви разнесения; [R] – корреляционная  матрица .

Каждый элемент матрицы |R| может быть найден из [ 19] и представлен в виде:

(4.36)

Где - разнос антенн j-й и k-й ветвей разнесения; β – волновое число;   и  - соответственно мощность шума и отношение несущая/шум в j-й ветви разнесения. Выражение (4.34) может быть упрощено [19 ]:

(4.37)

                                                                                                                                                                              

Где - собственные значения матрицы [R];

Подставляя (4.37) в (4.35) получим выражение для плотности распределения вероятностей

(4.38)

                                                                                                                                                                                 

Где собственные значения  могут быть либо положительными действительными числами, либо комплексно – сопряженными парами чисел. Функция распределения 𝜸 может быть записана как:

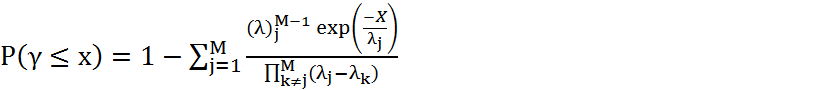(4.39)

Рассмотрим пример.

Дана линейная решетка с расстоянием между соседними элементами .

Решетки формирует 3 ветви разнесения. Найти собственные значения  корреляционной матрицы [R], полагая, что середина значения отношений несущая/шум в ветвях разнесения одинаковы (

Элементы корреляционной матрицы [R] могут быть найдены из выражения (4.36) и представлены как:

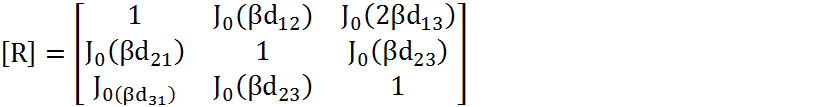(4.40)

                                                                                                                                                                                

Поскольку = ,

В силу четности 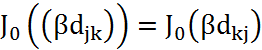, 𝝀 – длина волны функции Бесселя.

Тогда собственные значения корреляционной матрицы, составленной из элементов (4.40) могут быть найдены из уравнения

(4.41)

Где [I] – единичная матрица; - собственные значения матрицы.

Подставляя (4.40) в (4.41) можно получить матричное уравнение

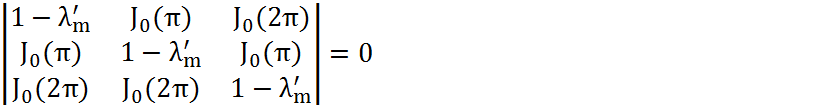(4.42)

Раскрывая уравнение (4.42) и полагая   и , получим

(4.43)

Где  и

Уравнение (4.43) можно проверить на выполнение условия

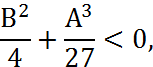
Которое показывает, что существует три действительных неравных корня, а именно

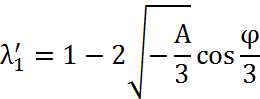
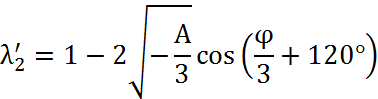
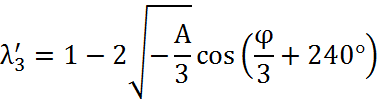
Где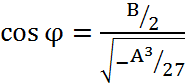

Рассмотрим случай – М-кратное сложение некоррелированных сигналов при условии, когда все значения  равны между собой (, тогда выражение (4.37) упрощается, а (4.35) принимает вид:

(4.44)

и функция распределения

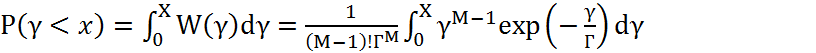(4.45)

При М=2 получаем

(4.46)

При М=3

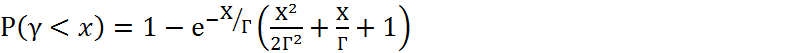(4.47)                                                                                                                                                                            

         Из анализа зависимостей (4.45 – 4.47) следует, что наибольшее улучшение характеристик сигнала наблюдается при переходе от системы без разнесения к системе с двукратным разнесением ,  как показано  на  рис.4.9.

Влияние корреляции рассмотрим на примере двукратного сложения сигналов.

Когда сигналы в двух ветвях разнесения коррелированны, то

(4.48)

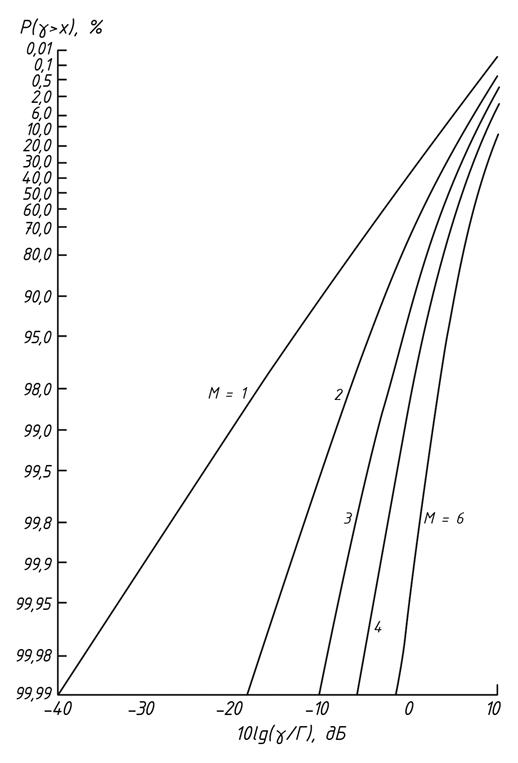
                                  Рис.4.9. Характеристики  комбинирования  сигналов  в  неза-

                                                висимых  ветвях разнесения  методом сложения,

                                                максимизирующего  отношение  сигнал - шум  

Где p – комплексный коэффициент корреляции двух гауссовских случайных величин.

Собственные значения являются решением следующего уравнения:

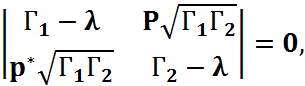
Тогда

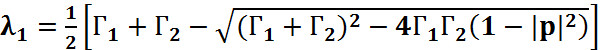                              (4.49)

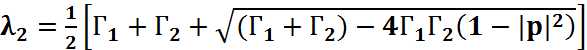                                (4.50)

Для  выражения (4.49)и (4.50) принимают вид:

Тогда выражение (4.38) примет вид:

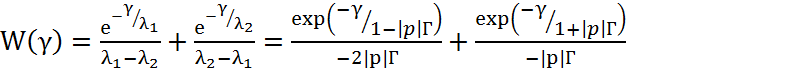(4.51)

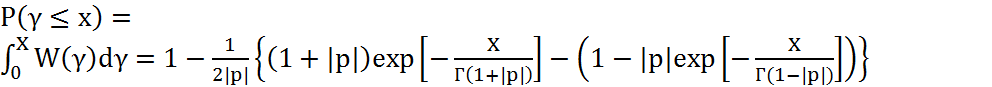(4.52)

Как видно из рис.4.10  при p=1 эффекта разнесения нет.