Теорема Котельникова

1.3.1. Теорема Котельникова.

Теорема Котельникова В.А. в 1938г.

Любой непрерывный сигнал  с ограниченным спектром может быть однозначно представлен (восстановлен) своими отсчетами взятыми через равные промежутки времени Δt, длительность которых не превышает половины периода верхней частоты его спектра fд ≥2fв.

Для техники связи важна возможность представления непрерывной функции времени или СП через совокупность их значений в дискретные моменты времени. Такую процедуру называют дискретизацией или квантованием сигнала по времени. Эта процедура применяется к сигналам с ограниченным спектром. Спектр всех реальных сигналов неограничен, но можно указать некоторую полосу частот, где сосредоточена основная часть мощности сигнала. Эта полоса  частот содержит всю существенно необходимую информацию о сообщении, заложенную в сигнале. Если остальную часть спектра сигнала не передавать, то это практически не отразится на точности его восстановление. В инженерной практике рассмотрение сигналов как функций с ограниченным спектром позволяет при проектировании аппаратуры связи ограничить ее полосу пропускания.

 На пример значение ширины спектра сигналов в каналах связи:

телефонного: 3 – 5кГц

вещания: 8 – 10 кГц

телевизионного: 8.5 МГц

Ограничение спектра сигнала происходит с помощью фильтра нижних частот. Спектр дискретизированного  сигнала является периодическим продолжением (с частотой дискретизации) спектра исходного сигнала.

   S(t)                                                              S(f)

 

                                                                                      

                                                                                             fв=fc                         f                                                                                                                                                                                                                                                      

S(k Δt)                                                        Sд(f)

 

	0  ∆t 2∆t    4∆t   6∆t    8∆t   10∆t  12∆t 14∆t 16∆t     t

 

                                                                                               fв            fд              f

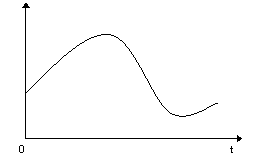
Так может быть представлен сигнал по теореме Котельникова:

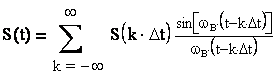
где S(k Δt) – отсчеты непрерывной функции в дискретных точках t=kΔt: