Помехоустойчивость системы связи с пространственно-временным кодированием в канале с частотно-селективными замираниями

Журович В.А., Капленко М.Ф., Сидельников Г.М.

Помехоустойчивость системы связи с пространственно-временным кодированием в канале с частотно-селективными замираниями

В современных системах связи, в частности, в системах мобильной радиосвязи, принципиальным требованием является максимально эффективное использование частотного ресурса, достижению которого в значительной степени способствует метод пространственного разнесения с использованием нескольких антенн как на передаче, так и на приёме. Подобные системы получили название систем со множественными входами и множественными выходами (many input many output - MIMO) [1], причём на передаче желательно излучать сигналы с каждой антенны на одной и той же несущей частоте.

Система MIMO предполагает необходимость разделения и сложения сигналов, пришедших от n передающих антенн на входы m приёмных антенн. Максимально возможный порядок разнесения M=n×m. Для реализации выигрыша от разнесения сигналов, как правило, предполагают применять соответствующие алгоритмы кодирования сигналов на передающей стороне и декодирования сигналов на приёмной стороне, используя данные о состоянии канала.

Данная работа посвящена анализу помехоустойчивости системы с пространственно-временным кодированием в канале с межсимвольной интерференцией (МСИ), вызванной многолучевым распространением, или для канала с частотно-селективными замираниями (полоса когерентности канала меньше полосы сигнала). Рассчитывается неустранимая вероятность ошибки для приёма сигналов ДОФМ.

Рассмотрим систему разнесённого приёма с пространственно-временным кодированием, когда используется на передаче n передающих антенн, а на приёме - m приёмных антенн.

На рис. 1 приведена такая система для четырёх передающих и четырёх приёмных антенн. В соответствии с алгоритмом кодирования [2], число передающих антенн может быть только чётным. Порядок передаваемых сигналов на передатчике в соответствии с алгоритмом представлен в виде матрицы [2]:

                                       

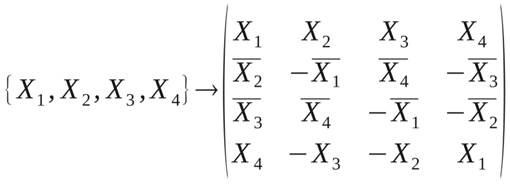
                                                                                          .                                 (1)

В момент времени t передаётся первая строка матрицы (1), в момент времени t+T - вторая строка (где T - длительность посылки), в момент t+2T - третья строка матрицы и т.д., при этом номер столбца - это номер антенны. Первая антенна (рис. 1) последовательно в разные моменты времени передаёт последовательность                                             , вторая антенна - последователь                                  и т.д.

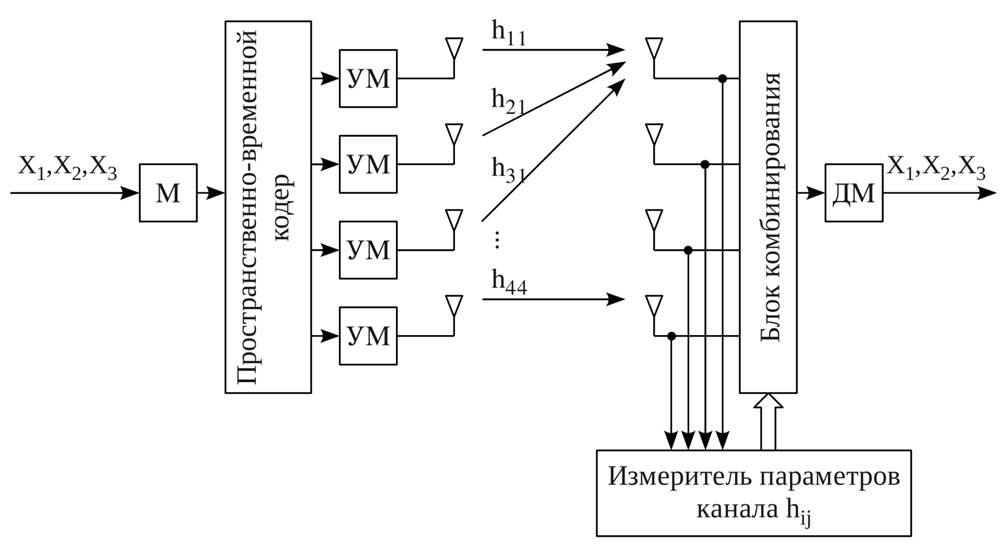Рисунок 1 - Структурная схема системы разнесённого приёма при пространственно-временном кодировании

На приёмной стороне может быть установлено любое число антенн, как чётное, так и нечётное. Так как в соответствии с алгоритмом Аламоути на передающей стороне может быть только чётное количество антенн, то при передаче последовательности из трёх элементов порядок передачи представляется как

                                       

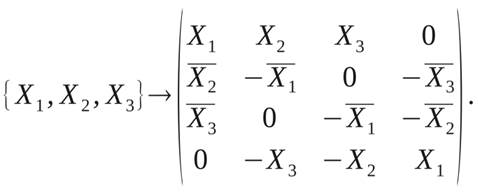
                                                                                                                            (2)

Таким образом, при кодировании трёх сигналов отсутствие четвёртого компенсируется только уменьшением общей мощности передатчика.

Рассмотрим порядок кодирования и декодирования сигналов при разнесённом приёме на примере двух передающих и одной приёмной антенны.

Сигналы на передаче в моменты времени t и t+T:

                                                                                

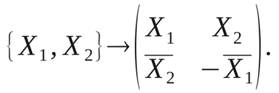
                                                                                                                                   (3)

На приёмной стороне в разные моменты времени (r₁ → t), (r₂ → (t+T)) с учётом коэффициента передачи

 

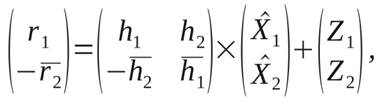                                                                                                                                   (4)

где Z₁ и Z₂ — вектор помехи, включающий в себя как аддитивный гауссовский шум, так и межсимвольную интерференцию,

r₁ и -r₂  - векторы сложения лучей в разные моменты моменты времени.

Схема комбинирования на приёмной стороне представляет собой

 

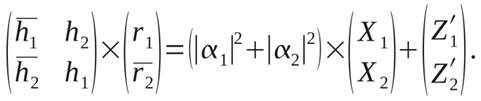                                                                                                                                   (5)

Если от матричной формы перейти к последовательной записи, то выражение (4) можно представить как

                                

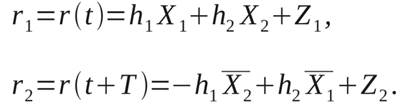
                                                                                                                            (6)

Выражение (5) можно представить как                                               

 

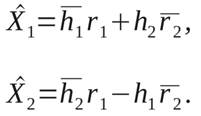                                                                                                                            (7)