Помехоустойчивость системы связи с пространственно-временным кодированием в канале с частотно-селективными замираниями, страница 2

Подставив (6) в (7), получим:

 

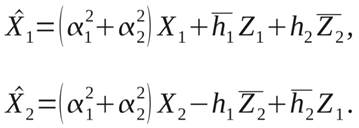                                                                                                                            (8)

Сигналы, полученные из выражения (8), поступают на демодулятор, на выходе из которого решающее устройство принимает решение о том, какой сигнал передавался с первой антенны, а какой со второй.

Таким образом, на вход демодулятора поступает сигнал, усиленный в

При использовании двух передающих и двух приёмных антенн, сигнал на входе демодулятора будет иметь вид:

 

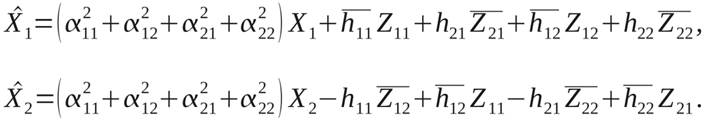                                                                                                                            (9)

                                                                                                                            (10)

Как видно из рассмотренных алгоритмов приёма, метод комбинирования сигналов при пространственно-временном кодировании можно характеризовать как сложение, максимизирующее отношение сигнал/шум. В общем виде лучи складываются с весом, прямо пропорциональным величине, комплексно сопряжённым с замирающим сигналом и обратно пропорциональным мощности шума в ветви разнесения.

В [1] приведены зависимости вероятности ошибки от отношения сигнал/шум при пространственно-временном кодировании для каналов с гладкими замираниями (полоса когерентности канала больше полосы сигнала). Поэтому в дальнейшем рассмотрим помехоустойчивость приведённых выше алгоритмов для сигналов ДОФМ для канала с частотно-селективными замираниями.

Сигнал на входе приёмника представим как

                                                   Y(f) = S(f)×H(f)+N(f),                                          

где H(f) - случайная функция передачи канала, которая предполагается комплексным гауссовским процессом, поскольку комплексные гауссовские характеристики канала могут быть достаточно определены [3].

Корреляционную функцию процесса H(f) часто называют частотной корреляционной функцией и определяют как

 

                                                                                                                                   (11)

Как показано в [4], для подвижных систем связи в условиях города выражение (11) имеет гауссовский характер:

 

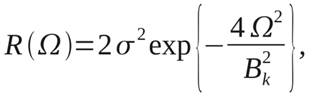                                                                                                                                   (12)

где B_k  - полоса когерентности (интервал корреляции), определяемая на уровне 1/е,

      - средняя мощность сигнала.

Функция задержек, определяемая как преобразование Фурье от (12):

 

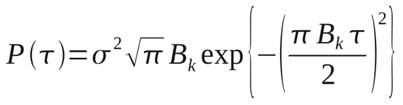                                                                                                  .                                (13)

Выражения (12) и (13) достаточно хорошо характеризуют канал, где определяющим параметром условий приёма является полоса когерентности B_k, при этом вид зависимости (13) в значительно меньшей степени влияет на помехоустойчивость системы с разнесением антенн.

Демодулятор сигналов ДОФМ представляет собой когерентный приёмник, на выходе из которого образуется сигнал:

 

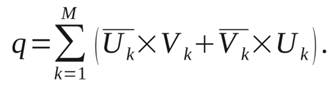Вероятность ошибки [3] определяется как

 

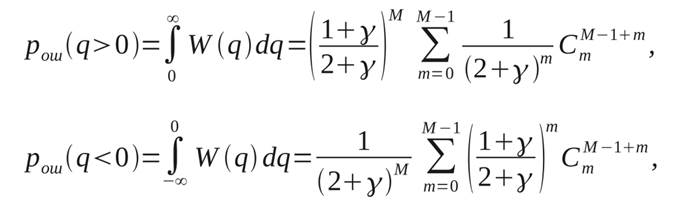                                                                                                                            (14)

                                                                                                                            (15)

где М - порядок разнесения (M=n×m).

Отношение сигнал/шум определяется как

 

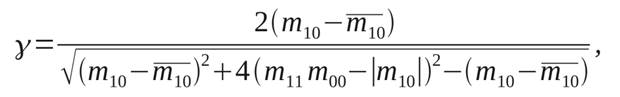                                                                                                                                   (16)

 

где

Сигналы прямой и задержанный соответственно:

 

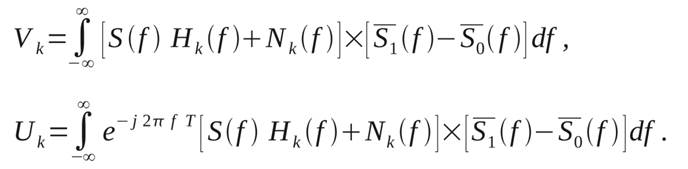                                                                                                                                   (17)

                                                                                                                                   (18)

Момент m_rs определяется как

 

                                                                                                                                   (19)

где:

 

                                                                                                                                   (20)

 

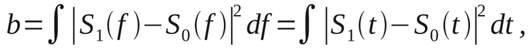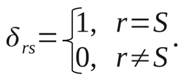Если ввести величину

 

выражение (20) может быть приведено к виду