Основы электротехники и электроники: Курс лекций, страница 9

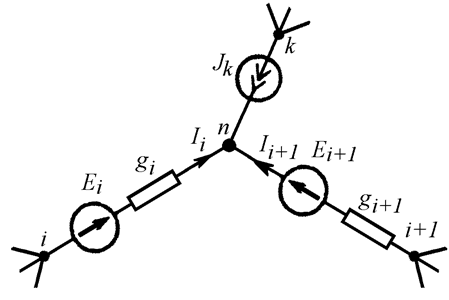
Рис. 13.3

Для узла n запишем первый закон Кирхгофа:

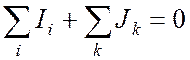                                                                     .              (13.1)

С другой стороны, по закону Ома для активного участка цепи:

                                                                  .           (13.2)

Подставим (13.2) в (13.1):

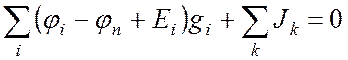                                                        . (13.3)

Перегруппируем слагаемые в (13.3):

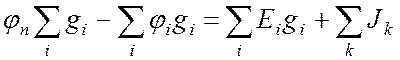                                                   .                                                                                (13.4)

Мы получили уравнение для потенциала произвольного узла цепи. Как видно, в нем фигурируют параметры ветвей, примыкающих к узлу, и потенциалы узлов, на которые опираются эти ветви.

Первый закон Кирхгофа позволяет получить независимые уравнения для всех узлов, кроме одного. Вместе с тем, потенциал определяется с точностью до произвольной постоянной. Следовательно, потенциал одного узла можно задать, например, приравнять нулю. В этом случае получим систему линейных алгебраических уравнений, имеющую единственное решение.

Пользуясь общим выражением (13.4), сформулируем алгоритм метода узловых потенциалов.

Алгоритм расчета цепи методом узловых потенциалов

1. Заземляется произвольный узел цепи, то есть его потенциал принимается равным нулю. Для укорочения уравнений целесообразно заземлять узел с наибольшим числом подходящих к нему ветвей. Если в цепи есть одна ветвь с нулевым сопротивлением и ЭДС, заземляется узел этой ветви. Потенциал второго узла этой ветви вычисляется автоматически. Если подобных ветвей несколько, необходимо их устранить вынесением ЭДС из ветви.
2. Для оставшихся узлов составляется система линейных алгебраических уравнений. Уравнение для каждого узла составляется так:

а)  потенциал узла умножается на сумму проводимостей, подходящих к узлу;

б)  из полученного произведения вычитаются потенциалы всех других узлов, умноженные на проводимости связующих ветвей;

в)  в правой части уравнения – алгебраическая сумма произведений ЭДС во всех ветвях, примыкающих к узлу, на проводимость своей ветви плюс сумма источников тока, примыкающих к узлу; с плюсом берутся источники тока и ЭДС, направленные к узлу, с минусом – противоположные.

3. После расчета потенциалов узлов определяются токи в ветвях по закону Ома и первому закону Кирхгофа. Ток в ветви с нулевым сопротивлением определить по закону Ома нельзя. В этом случае используется первый закон Кирхгофа.
4. Матрица системы уравнений симметрична относительно главной диагонали. Уравнения в системе имеют размерность тока.

Пример 13.1:

Определить токи методом узловых потенциалов (Рис. 13.4).

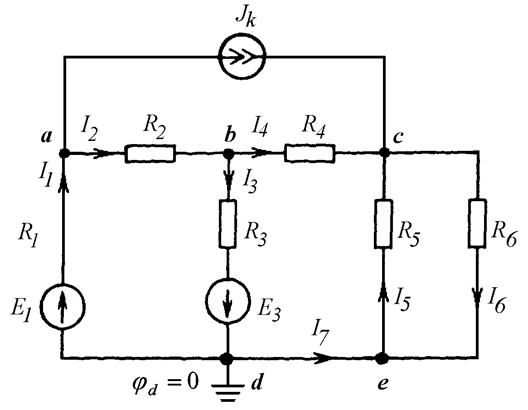
Рис. 13.4

Заземляем узел d:

.

Тогда автоматически определяются потенциалы узлов e и a. Потенциал узла e также равен нулю. ЭДС E₁ направлена от меньшего потенциала к большему, значит потенциал узла a больше потенциала узла d на величину ЭДС:

.

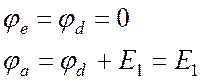Систему уравнений составляем для потенциалов узлов b и c:

.

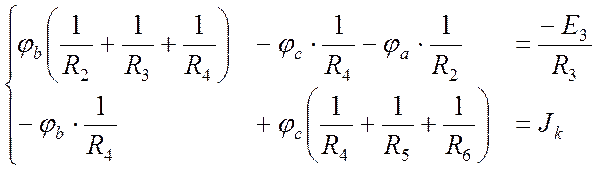Обратить внимание: в первом уравнении в левой части фигурирует потенциал узла a, так как узел a связан с узлом b ветвью с сопротивлением R₂.

Потенциал узла a известен, поэтому перенесем его в правую часть системы с противоположным знаком:

.

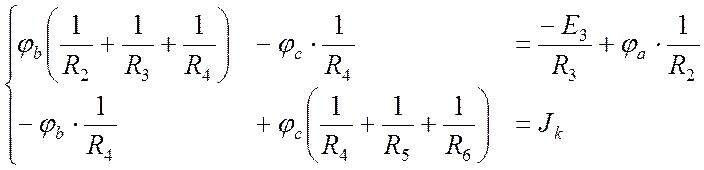После решения системы уравнений определяем токи по закону Ома и первому закону Кирхгофа. Чтобы правильно использовать закон Ома, расставим на схеме напряжения (Рис. 13.5):

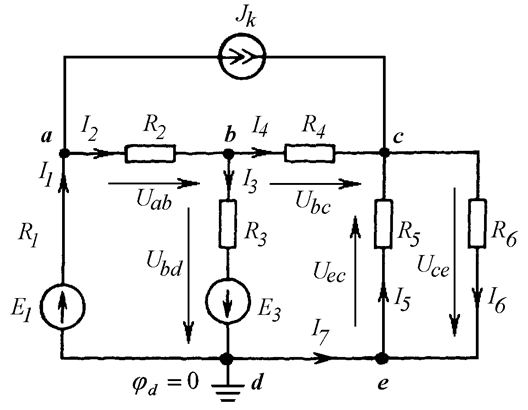
Рис. 13.5

Напряжения связаны с потенциалами следующими соотношениями:

.

.

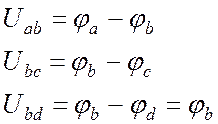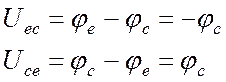Определяем токи по закону Ома:

.

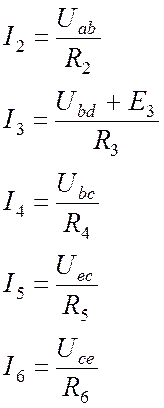Токи I₁ и I₇ определяем по первому закону Кирхгофа:

.

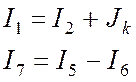Метод двух узлов

В том случае, если в цепи имеется всего два узла, использование метода узловых потенциалов приведет к одному уравнению, из которого сразу можно выразить напряжение между узлами.

Для цепи с двумя узлами (Рис. 13.6) составим уравнение по методу узловых потенциалов, приравняв нулю потенциал узла b:

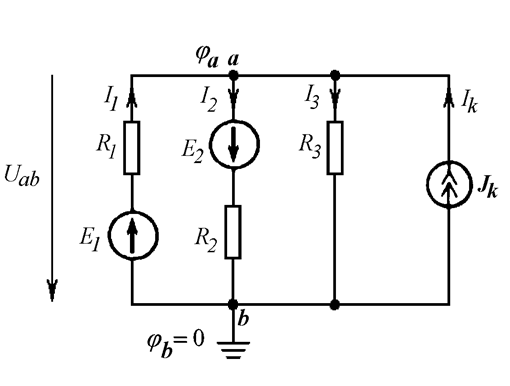
Рис. 13.6

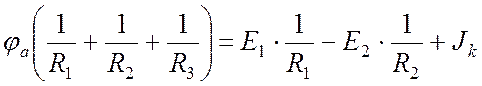                                           .                                                                                (13.5)

Так как напряжение между узлами:

                                                                   ,

из (13.5) получим:

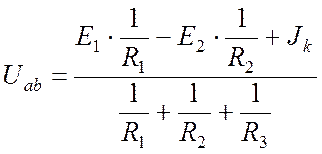                                                          .   (13.6)

Анализ формулы (13.6) позволяет обобщить ее для любой произвольной цепи с двумя узлами:

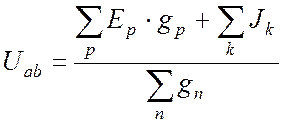                                                             .      (13.7)

В числителе выражения (13.7) – сумма источников тока плюс сумма произведений ЭДС на проводимость своей ветви. С плюсом берутся источники, направленные к узлу большего потенциала. В знаменателе – сумма проводимостей всех ветвей, как активных, так и пассивных.

Пример 13.2

Определить токи методом двух узлов (Рис. 13.7).

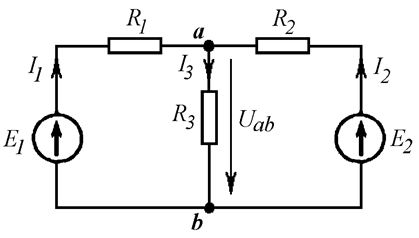
Рис. 13.7

В соответствии с методом двух узлов напряжение между узлами:

.

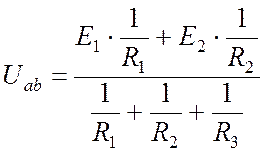Токи определяются по закону Ома:

.

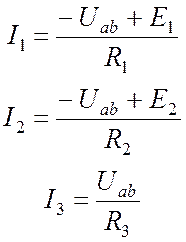14. ТЕОРЕМА О КОМПЕНСАЦИИ

Выделим из сложной схемы ветвь. Сложная цепь, рассматриваемая относительно какой-либо ветви, называется двухполюсником. Если внутри схемы есть источники энергии, двухполюсник называется активным (Рис. 14.1).

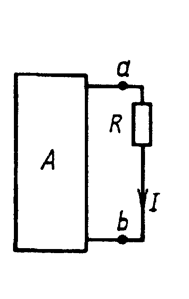
Рис. 14.1

Если в ветвь включить две одинаковые и противоположно направленные ЭДС (Рис. 14.2), то ни в самой ветви, ни в активном двухполюснике токораспределение не изменится.

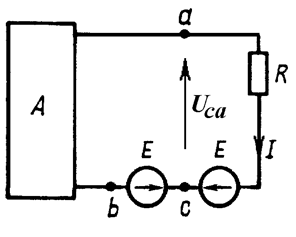
Рис. 14.2

По второму закону Кирхгофа запишем равенство:

                                                                      .               (14.1)

Так как ЭДС E может иметь любое произвольное значение, потребуем, чтобы выполнялось равенство:

                                                                            .                     (14.2)

Подставив (14.2) в (14.1), обнаружим, что

.

Напряжение между точками c и a равно нулю. Значит, потенциалы этих точек равны, и точки можно соединить (Рис. 14.3).

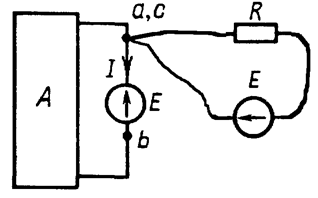
Рис. 14.3