Полупроизведение амплитуд напряжения и тока, без сомнения, равно произведению их действующих значений:
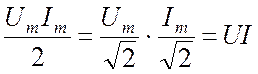 .
.
Тогда (19.4) будет выглядеть так:
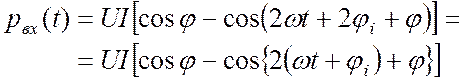 . (19.5)
. (19.5)
Преобразуем косинус суммы углов, используя формулу:
![]() .
.
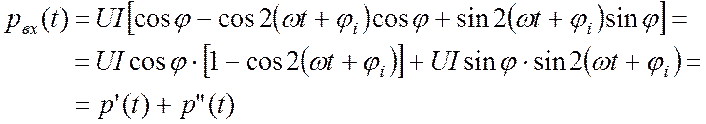 . (19.6)
. (19.6)
На Рис. 19.2
показаны кривые ![]() и
и ![]() .
Мощность
.
Мощность ![]() – это мощность полезной работы,
мощность
– это мощность полезной работы,
мощность ![]() – это мощность электромагнитного обмена
между источником и приемником энергии.
– это мощность электромагнитного обмена
между источником и приемником энергии.
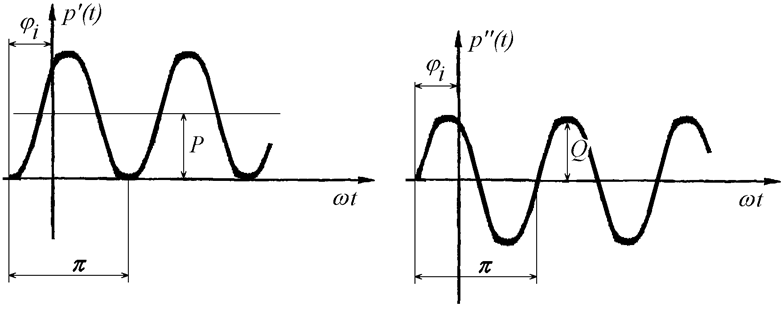
Рис. 19.2
Для оценки мощности требуются не мгновенные, а интегральные величины. В качестве таковых используются активная и реактивная мощность.
Под активной мощностью понимают среднее за период значение мощности полезной работы:
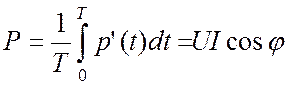 . (19.7)
. (19.7)
Под реактивной мощностью понимают максимальное значение, которого может достигать мощность электромагнитного обмена:
![]() . (19.8)
. (19.8)
На резисторе (Рис. 19.3)
напряжение и ток совпадают по фазе и угол ![]() равен
нулю. Следовательно, равна нулю и реактивная мощность. Поэтому резистор часто
называют активным сопротивлением.
равен
нулю. Следовательно, равна нулю и реактивная мощность. Поэтому резистор часто
называют активным сопротивлением.
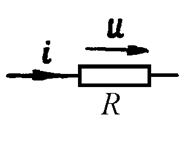
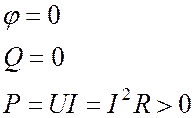
Рис. 19.3
На
индуктивности (Рис. 19.4) напряжение опережает ток на ![]() , поэтому угол
, поэтому угол ![]() равен
равен ![]() .
Активная мощность равна нулю, а реактивная мощность положительна.
.
Активная мощность равна нулю, а реактивная мощность положительна.
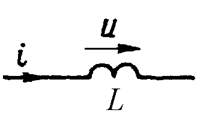
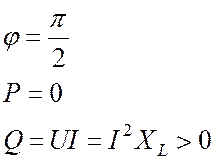
Рис. 19.4
На емкости (Рис. 19.5)
напряжение отстает от тока на ![]() , поэтому угол
, поэтому угол ![]() равен
равен 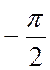 .
Активная мощность равна нулю, а реактивная мощность отрицательна.
.
Активная мощность равна нулю, а реактивная мощность отрицательна.
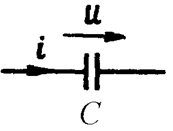
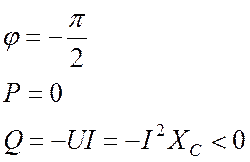
Рис. 19.5
Следует понимать, что знаки плюс и минус не означают направления или количественного значения реактивной мощности, так как мощность по своей физической природе – величина скалярная. Знак реактивной мощности показывает лишь положение фазы напряжения по отношению к фазе тока. Именно поэтому различают индуктивную и емкостную реактивную мощность.
Если
напряжение опережает ток, говорят, что реактивная мощность и ![]() имеют индуктивный характер. Если
напряжение отстает от тока, говорят, что реактивная мощность и
имеют индуктивный характер. Если
напряжение отстает от тока, говорят, что реактивная мощность и ![]() имеют емкостной характер.
имеют емкостной характер.
Для цепей переменного тока необходимо составлять два баланса: баланс активной и баланс реактивной мощности.
Баланс активной мощности:
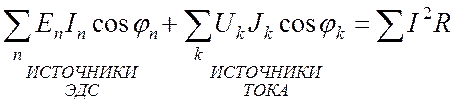 . (19.9)
. (19.9)
Баланс реактивной мощности:
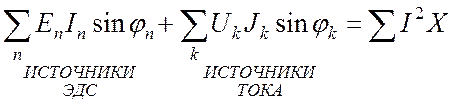 . (19.10)
. (19.10)
Следует иметь в виду, что при составлении баланса реактивной мощности в правой части выражения (19.10) необходимо учитывать знак мощности: индуктивная мощность имеет знак плюс, емкостная – минус.
Помимо активной и реактивной мощности широко используется такое понятие как полная мощность (иногда ее также называют кажущейся). Полная мощность определяется соотношением:
![]() . (19.11)
. (19.11)
Полная мощность равна произведению действующих значений тока и напряжения в ветви. Единица полной мощности – Вольт-Ампер (ВА).
Активная, реактивная и полная мощность связаны между собой соотношением:
![]() . (19.12)
. (19.12)
Графически эту связь можно изобразить в виде прямоугольного треугольника (Рис. 19.6).
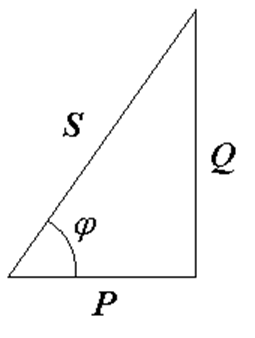
Рис. 19.6
Сравнивая треугольник мощностей с треугольниками токов, напряжений и сопротивлений, нетрудно обнаружить, что:
![]() , (19.13)
, (19.13)
где 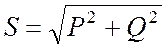
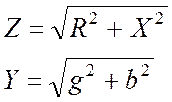
Также очевидны следующие соотношения:
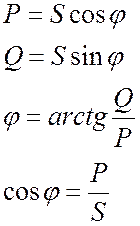 . (19.14)
. (19.14)
В выражениях
(19.14) фигурирует параметр ![]() . Его называют
коэффициентом мощности. Коэффициент мощности равен отношению активной мощности
к полной мощности.
. Его называют
коэффициентом мощности. Коэффициент мощности равен отношению активной мощности
к полной мощности.
Мощность синусоидального режима в комплексной форме
Чрезвычайно удобно рассчитывать мощность синусоидального режима в комплексной форме. Пусть напряжение на некотором участке цепи:
![]() . (19.15)
. (19.15)
Ток участка:
![]() . (19.16)
. (19.16)
При определении мощности надо знать угол между напряжением и током:
![]() .
.
Если комплекс
напряжения (19.15) умножить на комплекс, сопряженный с комплексом тока,
результирующее комплексное число будет содержать в себе разность (а не сумму)
углов ![]() и
и ![]() .
Это число и есть комплекс полной мощности:
.
Это число и есть комплекс полной мощности:
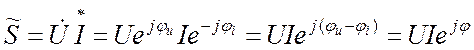 . (19.17)
. (19.17)
Знак ~ над комплексом полной мощности показывает, что, с одной стороны, полная мощность – это не синусоидальная функция времени (комплексы которых обозначаются точкой), с другой стороны – это и не параметр цепи (комплексы параметров цепи обозначаются здесь чертой под символом).
Как и всякое комплексное число, полную мощность можно представить в тригонометрической и алгебраической форме:
![]() . (19.18)
. (19.18)
Таким образом, в комплексной форме действительная часть полной мощности – это активная мощность, мнимая часть – реактивная мощность.
Пусть
комплексное сопротивление участка цепи равно ![]() ,
комплексный ток участка равен
,
комплексный ток участка равен ![]() . Тогда напряжение
участка по закону Ома:
. Тогда напряжение
участка по закону Ома:
![]() . (19.19)
. (19.19)
Подставим (19.19) в (19.17):
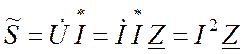 . (19.20)
. (19.20)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.