Электротехника \ Основы электротехники и электроники

Основы электротехники и электроники: Курс лекций, страница 10

Очевидно, что образовавшаяся петля – это замкнутый контур, который не оказывает влияния на токораспределение между точками a и b, и его можно вовсе удалить из схемы (Рис. 14.4).

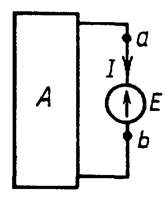
Рис. 14.4

Вышеприведенные рассуждения позволяют сделать следующий вывод: любое сопротивление в любой ветви схемы можно заменить эквивалентной ЭДС, численно равной падению напряжения на этом сопротивлении и направленной навстречу току.

Очевидно, что эту теорему можно сформулировать и следующим образом: любое сопротивление в любой ветви схемы можно заменить эквивалентным источником тока. Ток источника численно равен току через сопротивление и направлен в ту же сторону.

15. МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА

Рассмотрим произвольную электрическую цепь, представив ее в виде активного двухполюсника и ветви (Рис. 15.1).

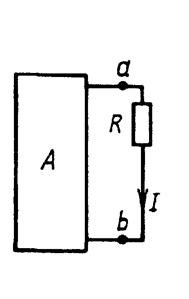
Рис. 15.1

Как и в предыдущей задаче, мы можем включить в ветвь две равных и противоположно направленных ЭДС. Это не изменит токораспределения в схеме (Рис. 15.2).

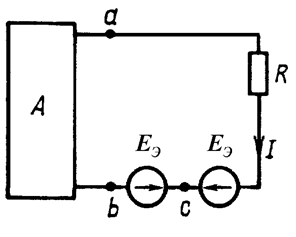
Рис. 15.2

Воспользовавшись методом наложения, разобьем получившуюся цепь на две: в одной из них оставим лишь одну ЭДС Eэ (при этом двухполюсник станет пассивным), в другой оставим все остальные источники (Рис. 15.3).


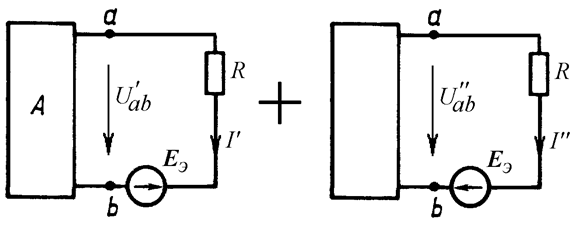
Рис. 15.3

Реальный ток ветви есть сумма двух составляющих:

                                                                            .                    (15.1)

По закону Ома можно определить ток :

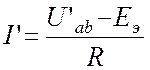                                                                        .                 (15.2)

Так как ЭДС Eэ можно выбрать произвольно, выберем ее так, чтобы дробь (15.2) обращалась в нуль.

                                               При               .                (15.3)

Соотношение (15.3) означает, что активный двухполюсник на Рис. 15.3 работает в режиме холостого хода, то есть ветвь с сопротивлением R разомкнута или вообще удалена из схемы (Рис. 15.4). Напряжение  называют напряжением холостого хода.

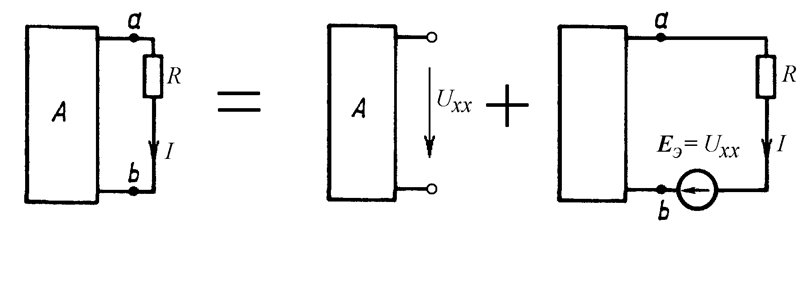
Рис. 15.4

Любой пассивный двухполюсник всегда можно свернуть в одно эквивалентное сопротивление. Тогда исходная схема принимает вид (Рис. 15.5):

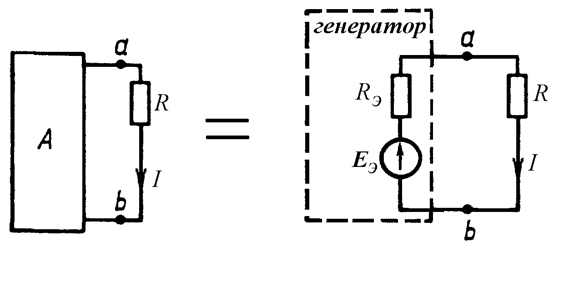
Рис. 15.5


Ток в ветви определяется по закону Ома:

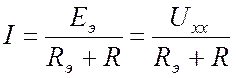                                                                 ,          (15.4)

где      Eэ – ЭДС эквивалентного генератора;

            Rэ – сопротивление эквивалентного генератора;

            R – сопротивление ветви с искомым током.

Как видно из предыдущих рассуждений ЭДС эквивалентного генератора численно равна напряжению в разрыве ветви с искомым током и направлена в сторону тока. Сопротивление эквивалентного генератора – это сопротивление цепи, из которой удалены все источники энергии, свернутой относительно ветви с искомым током.

ЭДС и сопротивление эквивалентного генератора можно определить как экспериментально, так и аналитически.

Алгоритм экспериментального определения параметров эквивалентного генератора

  1. Разрывают ветвь с искомым током. Этот режим называется режимом холостого хода. Измеряют напряжение в разрыве. Оно направлено в ту же сторону, что и искомый ток и численно равно ЭДС эквивалентного генератора.
  2. Закорачивают ветвь с искомым током. Этот режим называется режимом короткого замыкания. Измеряют ток в закоротке. Этот ток называется током короткого замыкания.
  3. Сопротивление эквивалентного генератора равно отношению напряжения холостого хода к току короткого замыкания:

.

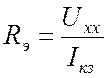Алгоритм аналитического расчета цепи методом эквивалентного генератора

  1. Ветвь с искомым током удаляется из схемы и заменяется двумя зажимами. Исходная цепь значительно упрощается. В дальнейшем ни в коем случае нельзя терять зажимы сворачиваемой схемы.
  2. Любым известным методом определяется напряжение между зажимами Uхх. Оно направлено в ту же сторону, что и искомый ток. ЭДС эквивалентного генератора равна этому напряжению.
  3. Вся цепь делается пассивной, то есть источники удаляются и заменяются своими внутренними сопротивлениями. Получившаяся пассивная цепь сворачивается в одно сопротивление Rэ относительно зажимов.
  4. Искомый ток определяется по закону Ома:

.

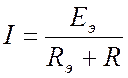Метод эквивалентного генератора наиболее эффективен, когда требуется определить ток в одной ветви с переменным сопротивлением.

Пример 15.1

Определить ток I3 методом эквивалентного генератора (Рис. 15.6).

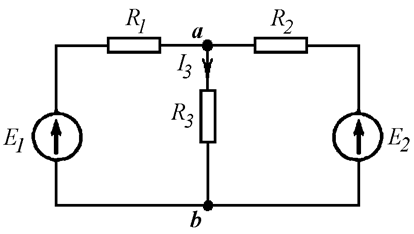
Рис. 15.6

Формируем схему режима холостого хода. Ветвь с искомым током удаляем из схемы. Заменяем ее двумя зажимами. Между зажимами обозначаем напряжение холостого хода. Оно направлено в ту же сторону, что и искомый ток (Рис. 15.7).

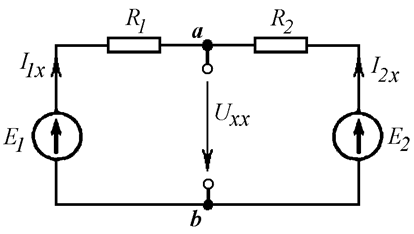
Рис. 15.7

По второму закону Кирхгофа для левого контура

.

По закону Ома находим ток:

.

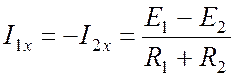После чего можно найти напряжение холостого хода:

.

ЭДС эквивалентного генератора равна напряжению холостого хода:

.

Определяем сопротивление эквивалентного генератора относительно зажимов (Рис. 15.8):

.

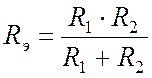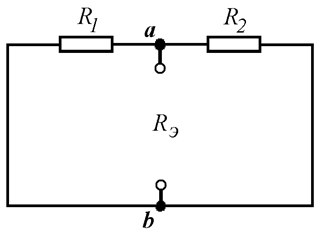
Рис. 15.8

Находим ток I3:

.


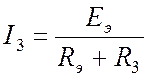16. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рис. 16.1):

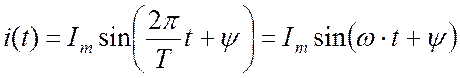                                              .                                                                                (16.1)

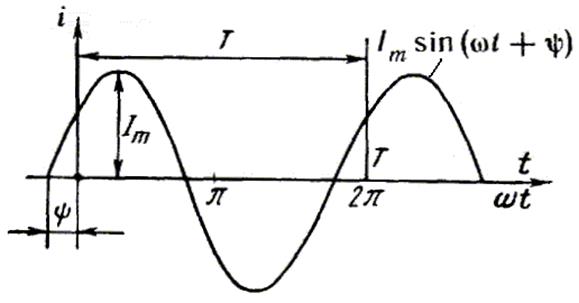
Рис. 16.1

Максимальное значение функции называют амплитудой. Амплитуду тока обозначают Im.

Период Т - это время, за которое совершается одно полное колебание.

Частота равна числу колебаний в одну секунду (единица частоты – герц (Гц) или с-1):

.

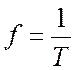Угловая частота (единица угловой частоты – рад/с или с-1):

.

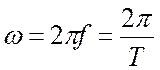Аргумент синуса, то есть , называют фазой, слагаемое  – начальной фазой.

Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.

Значение функции (16.1) в любой произвольный момент времени называют мгновенным значением.

Скачать файл