Основы электротехники и электроники: Курс лекций, страница 13

Символический метод позволяет перейти от графоаналитических расчетов с помощью векторных диаграмм к расчетам аналитическим. Это, с одной стороны, повышает точность расчетов, а с другой – значительно облегчает выполнение математических операций с синусоидальными функциями. Кроме того, символический метод позволяет без ограничений использовать для расчета цепей синусоидального тока все законы и методы, полученные для цепей постоянного тока.

Основная идея метода состоит в перенесении известной нам векторной диаграммы на комплексную плоскость. Пусть на комплексной плоскости со скоростью  вращается против часовой стрелки вектор, изображающий синусоидальную функцию тока (Рис. 18.1). Тогда этому вектору можно поставить в соответствие некоторую комплексную функцию, которая, как и вектор, будет изображением реального синусоидального тока.

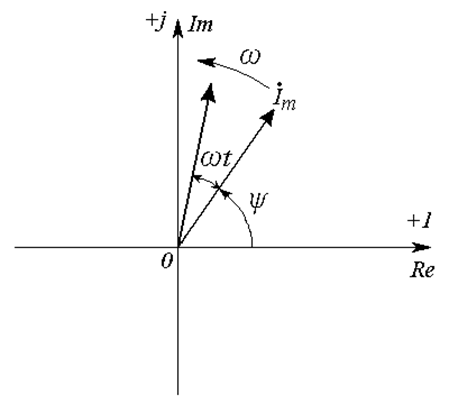
Рис. 18.1

Сразу заметим, что в теоретической электротехнике принято обозначать мнимую единицу (то есть квадратный корень из минус единицы) буквой j (читается по-немецки, «йот»), чтобы не путать ее с обозначением тока.

Также все комплексные величины, изображающие токи, напряжения и мощности, принято обозначать прописной буквой с точкой сверху. Комплексные величины, изображающие параметры цепи (сопротивления, проводимости), принято обозначать прописной буквой, подчеркнутой снизу. Модуль комплексного числа будем обозначать прописной буквой, без точки и черты.

Если функция тока имеет вид:

                                                                  ,          (18.1)

то изображающая ее комплексная функция:

  .                                                                                (18.2)

Очевидно, что исходная синусоидальная функция (18.1) совпадает с мнимой частью комплексной функции (18.2).

Как правило, в цепях действуют источники одной и той же частоты, поэтому нет необходимости вращать векторы. А это означает, что сомножитель  в (18.2), содержащий время, можно опустить и оперировать не с комплексной функцией, а с фиксированным комплексным числом.

Итак, все реальные синусоидальные функции заменяются комплексными числами. Расчеты проводятся в комплексной форме. Окончательный результат переводится в синусоидальную форму.

Заметим, что чаще всего при расчетах используются не амплитудные, а действующие значения токов и напряжений. Следует придерживаться этого правила.

Рассмотрим некоторые свойства комплексных чисел.

Как известно, любое комплексное число можно изобразить точкой на комплексной плоскости. В зависимости от способа описания координат этой точки можно выделить две формы комплексного числа – алгебраическую и показательную.

Алгебраическая форма комплексного числа соответствует декартовой системе координат на комплексной плоскости (Рис. 18.2):

                                                                          ,                   (18.3)

где      a – действительная часть числа (координата по оси Re);

            b – мнимая часть числа (координата по оси Im).

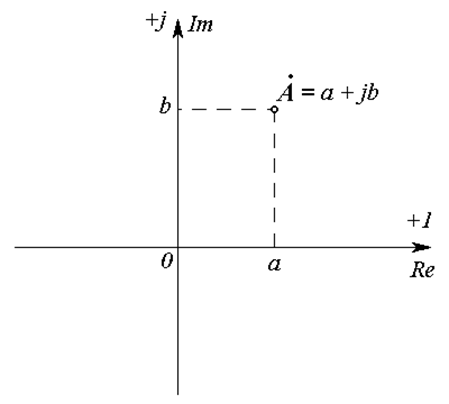
Рис. 18.2

Показательная форма комплексного числа соответствует полярной системе координат на комплексной плоскости (Рис. 18.3):

                                                                           ,                    (18.4)

где      A – модуль комплексного числа (длина радиус-вектора, соединяющего начало координат

            с точкой );

            Ψ – угол комплексного числа (откладывается от положительной полуоси действительных

            чисел; против часовой стрелки – со знаком плюс, по часовой стрелке – со знаком минус).

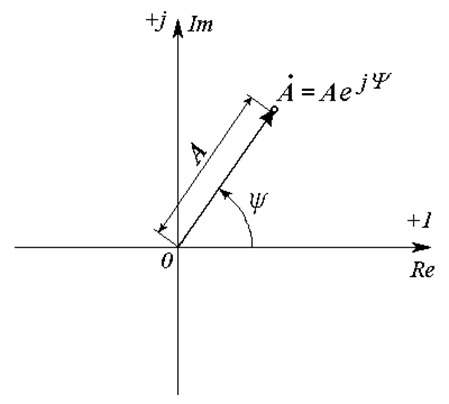
Рис. 18.3

Алгебраическая и показательная формы связаны друг с другом через тригонометрическую форму комплексного числа:

                                                                .         (18.5)

Из (18.5) выводятся формулы для перевода комплексного числа из одной формы в другую.

При переводе комплексного числа из показательной формы в алгебраическую используют соотношения:

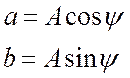                                                                          .                   (18.6)

При переводе комплексного числа из алгебраической формы в показательную используют соотношения:

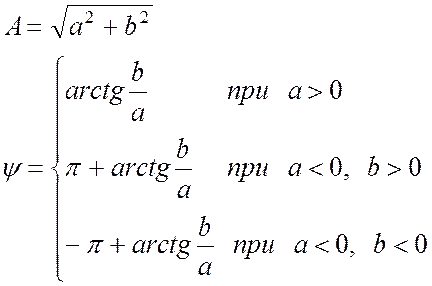                                                 .                                                                                (18.7)

Умножение комплексного числа на  эквивалентно повороту вектора на угол , так как 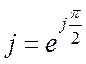 (Рис. 18.4).

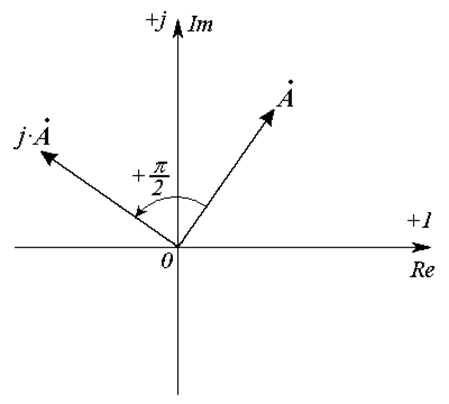
Рис. 18.4

Умножение комплексного числа на  эквивалентно повороту вектора на угол 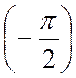, так как  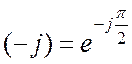(Рис. 18.5).

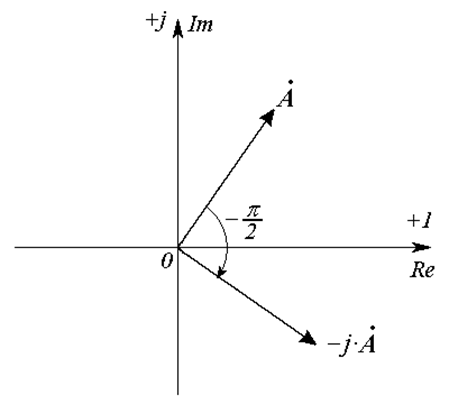
Рис. 18.5

Умножение комплексного числа на  эквивалентно повороту вектора на угол (или , что одно и то же), так как  (Рис. 18.6).

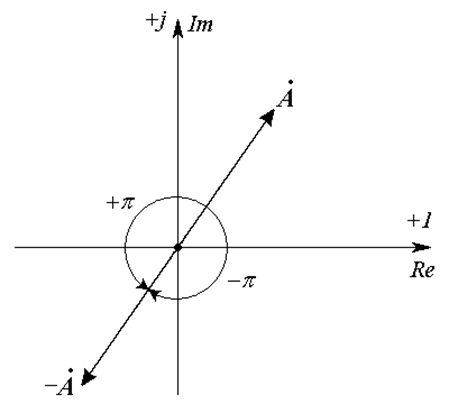
Рис. 18.6

Дифференцирование синусоидальной функции соответствует умножению ее комплексного изображения на :

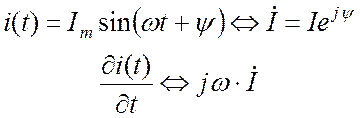                                                       .                                                                                (18.8)

Интегрирование синусоидальной функции соответствует делению ее комплексного изображения на :

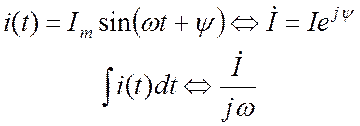                                                       .                                                                                (18.9)

Если в знаменателе дроби стоит чисто мнимое число (то есть число, действительная часть которого равна нулю), мнимая единица переносится в числитель путем умножения числителя и знаменателя на  (здесь используется равенство ), например:

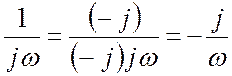                                                                 .        (18.10)

Если в знаменателе дроби стоит число с неравной нулю действительной частью, числитель и знаменатель дроби умножают на комплексно-сопряженное число. Комплексно-сопряженным числом называют число, симметричное данному относительно действительной оси (Рис. 18.7). Обозначается звездочкой сверху.

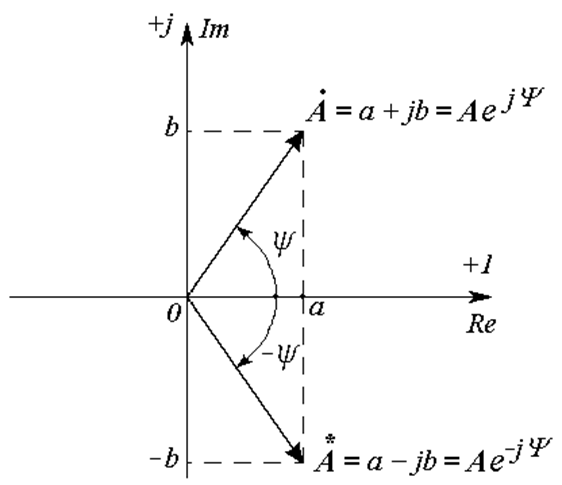
Рис. 18.7

Здесь используется известное равенство:

.

Произведение двух комплексно-сопряженных чисел равно квадрату их модуля.

Для переноса мнимой единицы в числитель умножим числитель и знаменатель на комплексно-сопряженное число: