Основы электротехники и электроники: Курс лекций, страница 11

Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов. Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов.

Мгновенное значение тока не определяет энергетических показателей переменного тока. Поэтому для оценки переменного тока используются такие интегральные характеристики, как среднее и действующее значение переменного тока.

Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока

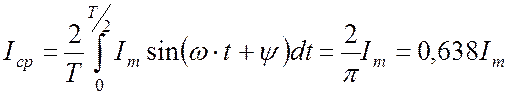                                       .                                                                                (16.2)

Аналогично вычисляются средние значения ЭДС и напряжения:

,

.

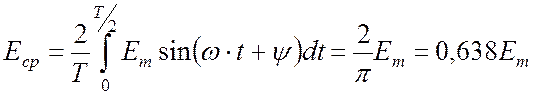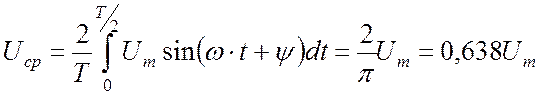Действующее значение тока (его называют также среднеквадратичным и эффективным) определяется как

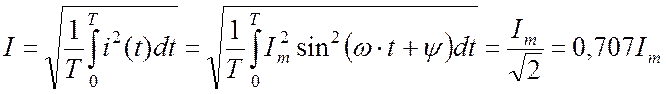             .                                                                                (16.3)

Аналогично вычисляются действующие значения ЭДС и напряжения:

,

.

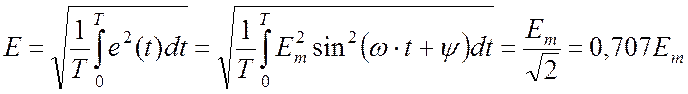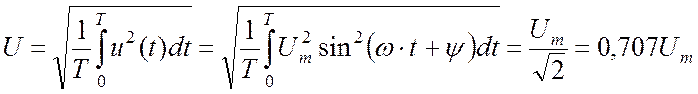Действующее значение – это чрезвычайно важная характеристика синусоидального тока, так как с ее помощью вводят соответствие между синусоидальным током и постоянным током. Именно поэтому действующие значения ЭДС, тока и напряжения обозначают такими же символами, что применяются для постоянных ЭДС, тока и напряжения (прописными буквами без индексов). Мгновенные значения ЭДС, тока и напряжения обозначают строчными буквами.

Сопоставим тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению R.

Количество теплоты, выделенное за один период синусоидальным током:

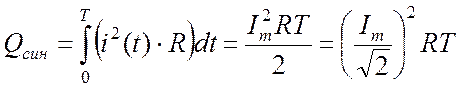                                              .                                                                                (16.4)

Выделенная за то же время постоянным током теплота равна:

                                                                       .                (16.5)

Множитель 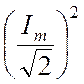 в (16.4) – это квадрат действующего значения синусоидального тока. Сопоставляя выражения (16.4) и (16.5), приходим к заключению, что действующее значение синусоидального тока равно значению такого постоянного тока, который за период синусоидального тока выделяет такое же количество теплоты.

Протекание синусоидальных токов по участкам электрической цепи сопровождается потреблением энергии от источников, а значит, и мощностью. Под мгновенной мощностью понимают произведение мгновенного значения напряжения на участке цепи на мгновенное значение тока, протекающего по этому участку:

                                                                      .               (16.6)

Рассмотрим соотношения между токами и напряжениями в простейших цепях. Элементами реальных цепей синусоидального тока являются резисторы, индуктивные катушки и конденсаторы. Протеканию синусоидального тока оказывают сопротивление резистивные элементы (резисторы) – в них выделяется энергия в виде теплоты – и реактивные элементы (индуктивные катушки и конденсаторы) – они то запасают энергию, то отдают ее.

Как уже отмечалось выше, резистор в электрической цепи моделирует преобразование электрической энергии в тепло. Его характеризуют зависимостью напряжения u от протекающего по нему тока i (вольт-амперной характеристикой) или сопротивлением. В линейных цепях синусоидального тока сопротивление резисторов постоянно:

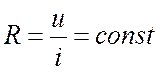                                                                       .                (16.7)

Пусть ток в цепи известен:

                                                                      .               (16.8)

В каждый произвольный момент времени напряжение на резисторе по закону Ома равно произведению тока на сопротивление. Если цепь линейна, напряжение на резисторе можно определить, перемножив выражения (16.7) и (16.8):

                                                .                                                                                (16.9)

Как видно из полученного выражения (16.9), в резистивном элементе напряжение и ток совпадают по фазе.

Чтобы найти мгновенную мощность, подставим (16.8) и (16.9) в (16.6):

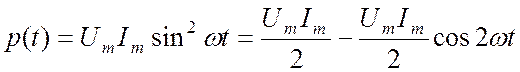                                     .                                                                               (16.10)

На Рис. 16.2 представлены кривые тока, напряжения и мгновенной мощности в резистивном элементе. Мгновенная мощность всегда положительна или равна нулю. Это означает, что резистор только потребляет энергию, но не отдает ее.

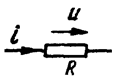
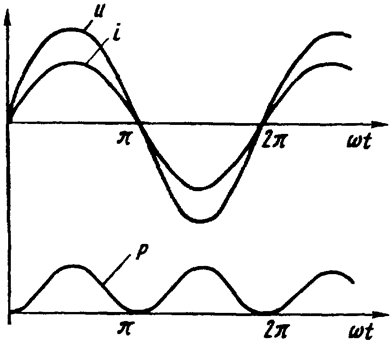
Рис. 16.2

Как правило, мощность в резисторе оценивают как среднее значение мгновенной мощности за период:

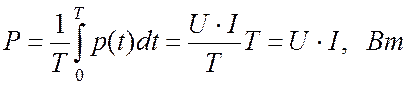                                                   .                                                                               (16.11)

Мощность в резисторе (16.11), называется активной. Ее размерность – Ватт.

Индуктивный элемент (катушка индуктивности) позволяет учитывать наведение ЭДС посредством изменения магнитного потока. Его характеризуют зависимостью потокосцепления ψ от тока i (вебер-амперной характеристикой) или индуктивностью. В линейных цепях индуктивность постоянна:

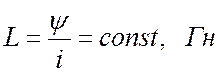                                                                  .         (16.12)

Размерность индуктивности – Генри.

При изменении магнитного потока в индуктивности возникает ЭДС самоиндукции, которая препятствует этому изменению:

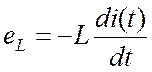                                                                        .               (16.13)

Подставим в (16.13) выражение для синусоидального тока (16.8):

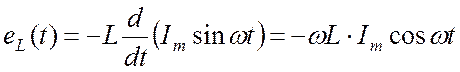                                              .                                                                               (16.14)

Напряжение на индуктивности направлено встречно ЭДС самоиндукции:

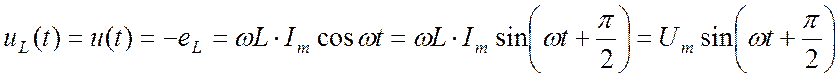.                                                                              (16.15)

Анализируя выражение (16.15) находим, что на индуктивности кривая напряжения опережает кривую тока на угол . Таким образом, индуктивность является фазосдвигающим элементом.