На оси ординат отмечаем точку, соответствующую заданному значению ЭДС E. Из точки E на оси ординат опускаем перпендикуляр до пересечения с вольт-амперной характеристикой эквивалентного нелинейного элемента. Эта точка называется рабочей точкой (Рис. 26.5 б). Абсцисса рабочей точки соответствует искомому току I*. Ток I* найден, задача решена.
Пример 26.2
В нелинейной цепи (Рис. 26.6 а) параллельно соединены два нелинейных элемента, вольт-амперные характеристики которых известны (Рис. 26.6 б). Требуется найти ток I* при заданной ЭДС E.
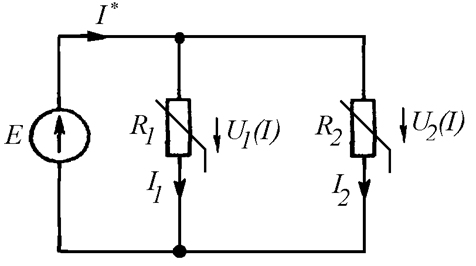
а)
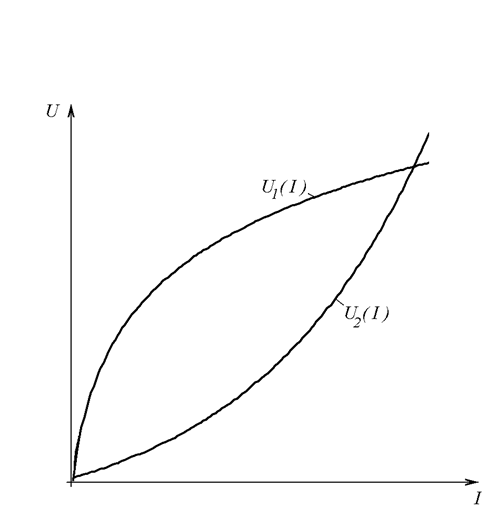
б)
Рис. 26.6
Уравнение по первому закону Кирхгофа имеет вид:
![]() . (Пр. 26.2.1)
. (Пр. 26.2.1)
К двум нелинейным элементам приложено одно и то же напряжение, равное ЭДС E. При этом токи нелинейно зависят от приложенного напряжения.
Заменим два нелинейных элемента одним эквивалентным (Рис. 26.7).
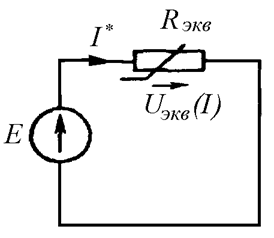
Рис. 26.7
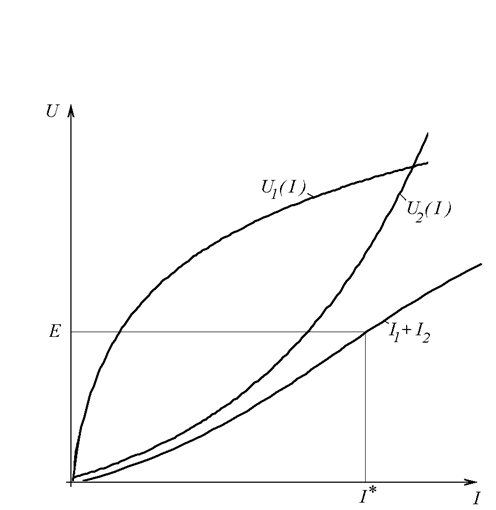
Как видно из первого закона Кирхгофа (Пр. 26.2.1), при параллельном соединении нелинейных элементов токи в них складываются. Значит, при построении вольт-амперной характеристики эквивалентного нелинейного элемента надо складывать абсциссы графиков U1(I) и U2(I) при фиксированных значениях напряжения (Рис. 26.8 а).
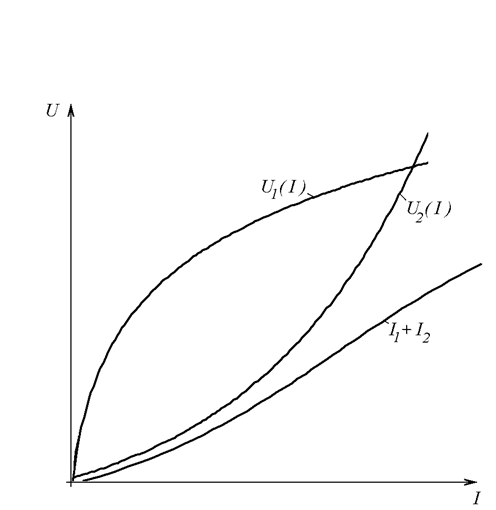
а)
б)
Рис. 26.8
На оси ординат отмечаем точку, соответствующую заданному значению ЭДС E. Из точки E на оси ординат опускаем перпендикуляр до пересечения с вольт-амперной характеристикой эквивалентного нелинейного элемента и находим рабочую точку (Рис. 26.8 б). Абсцисса рабочей точки соответствует искомому току I*. Ток I* найден, задача решена.
Метод кусочно-линейной аппроксимации
В методе кусочно-линейной аппроксимации реальный нелинейный элемент заменяется несколькими линейными, причем различным участкам реальной вольт-амперной характеристики нелинейного элемента соответствуют разные значения линейного сопротивления.
Пример 26.3
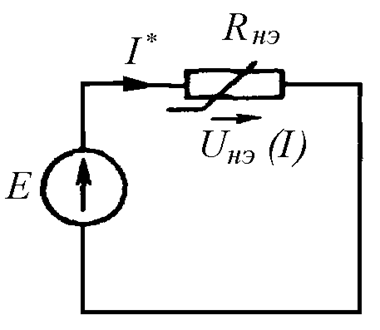
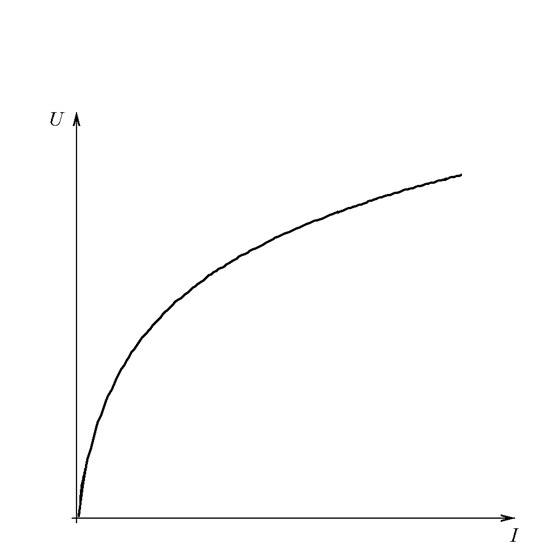
В цепи с одним нелинейным элементом (Рис. 26.9 а) требуется найти ток I* при заданной ЭДС E. Вольт-амперная характеристика нелинейного элемента известна (Рис. 26.9 б).
а)
б)
Рис. 26.9
Реальную
вольт-амперную характеристику нелинейного элемента заменим эквивалентной ломаной,
состоящей из двух прямых (Рис. 26.10, выделена красным цветом).
Первая прямая наклонена к оси абсцисс под углом ![]() ,
вторая прямая наклонена к оси абсцисс под углом
,
вторая прямая наклонена к оси абсцисс под углом ![]() .
Прямые, пересекаясь, образуют точку излома эквивалентной вольт-амперной
характеристики. Отметим на оси абсцисс ток
.
Прямые, пересекаясь, образуют точку излома эквивалентной вольт-амперной
характеристики. Отметим на оси абсцисс ток ![]() ,
соответствующий точке излома.
,
соответствующий точке излома.
На участке до
точки излома тангенс угла наклона прямой не изменяется. Значит, этому участку
соответствует неизменное линейное сопротивление ![]() .
В точке излома тангенс угла наклона изменяется скачком и в дальнейшем остается
постоянным. Значит, участку после точки излома соответствует неизменное
линейное сопротивление
.
В точке излома тангенс угла наклона изменяется скачком и в дальнейшем остается
постоянным. Значит, участку после точки излома соответствует неизменное
линейное сопротивление ![]() .
.
Таким образом, эквивалентное сопротивление цепи можно представить в виде кусочно-линейной функции, принимающей два значения в зависимости от тока в цепи:
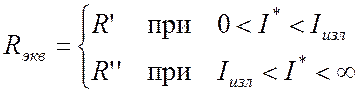 . (Пр. 26.3.1)
. (Пр. 26.3.1)
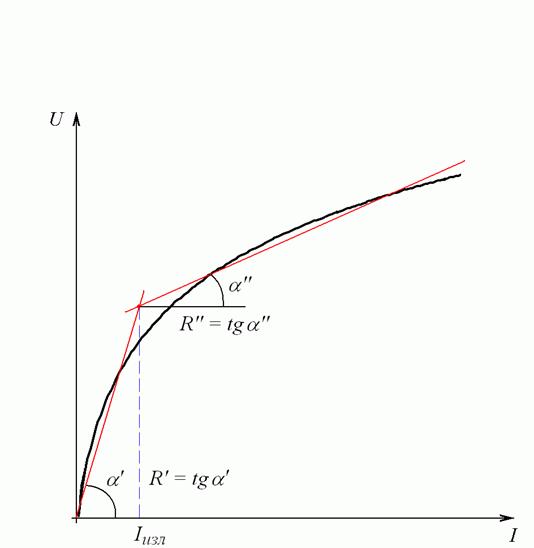
Рис. 26.10
При этом
реальная цепь заменяется цепью с одним линейным элементом, сопротивление
которого равно ![]() или
или ![]() в зависимости от того, на каком
участке вольт-амперной характеристики находится рабочая точка (Рис. 26.11).
Так как до расчета мы ничего не знаем о положении рабочей точки, придется
рассчитать цепь дважды с двумя значениями сопротивления, после чего выбрать то
значение тока I*, которое
удовлетворяет кусочной функции (Пр. 26.3.1), задающей сопротивление цепи.
в зависимости от того, на каком
участке вольт-амперной характеристики находится рабочая точка (Рис. 26.11).
Так как до расчета мы ничего не знаем о положении рабочей точки, придется
рассчитать цепь дважды с двумя значениями сопротивления, после чего выбрать то
значение тока I*, которое
удовлетворяет кусочной функции (Пр. 26.3.1), задающей сопротивление цепи.
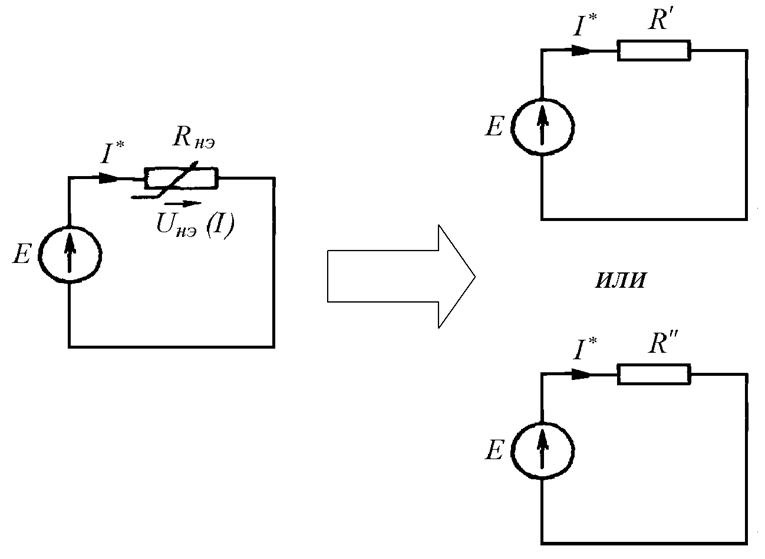
Рис. 26.11
27. МАГНИТНЫЕ ЦЕПИ
Для расчета магнитных цепей используют аналогию с нелинейными электрическими цепями постоянного тока. Вместе с тем, магнитным цепям присущи определенные особенности, заставляющие выделять магнитные цепи в самостоятельный раздел.
В теории электрических цепей основополагающими законами являются законы Кирхгофа, связывающие силовые характеристики источников и приемников электрической энергии с топологией цепи, то есть с тем, как источники и приемники электрической энергии соединяются друг с другом. Поэтом законы Кирхгофа называют также топологическими законами. Топологические законы позволяют при исследовании и расчете электрических цепей не пользоваться аппаратом теории электромагнитного поля. При рассмотрении же магнитных цепей без теории поля обойтись нельзя. Поэтому необходимо остановиться на основных понятиях теории магнитного поля, которые будут использоваться нами при расчетах магнитных цепей.
Основной
силовой характеристикой магнитного поля является индукция ![]() . Индукция магнитного поля – это
векторная величина, определяемая по силовому воздействию на проводник с током,
помещенный в магнитное поле. Индукция
. Индукция магнитного поля – это
векторная величина, определяемая по силовому воздействию на проводник с током,
помещенный в магнитное поле. Индукция ![]() считается
основной силовой характеристикой именно потому, что ее можно определить
непосредственным измерением. Единица индукции магнитного поля – Тесла (Тл).
считается
основной силовой характеристикой именно потому, что ее можно определить
непосредственным измерением. Единица индукции магнитного поля – Тесла (Тл).
Действие
внешних источников магнитного поля определяется напряженностью магнитного поля ![]() . Напряженность магнитного поля –
также векторная величина. Единица напряженности магнитного поля – Ампер,
деленный на метр (А/м).
. Напряженность магнитного поля –
также векторная величина. Единица напряженности магнитного поля – Ампер,
деленный на метр (А/м).
Индукция и напряженность магнитного поля связаны между собой соотношением:
![]() , (27.1)
, (27.1)
где ![]() –
магнитная постоянная, она же магнитная проницаемость вакуума;
–
магнитная постоянная, она же магнитная проницаемость вакуума;
![]() – относительная магнитная
проницаемость вещества (безразмерная величина).
– относительная магнитная
проницаемость вещества (безразмерная величина).
При решении большинства электротехнических задач вещества разделяют на две группы:
1) вещества,
относительная магнитная проницаемость которых равна единице, ![]() ; к таким веществам относятся воздух
(и вакуум), медь, алюминий и т. п.;
; к таким веществам относятся воздух
(и вакуум), медь, алюминий и т. п.;
2) вещества,
относительная магнитная проницаемость которых много больше единицы, ![]() ; к таким веществам относятся,
например, ферромагнетики железо, никель, кобальт и их сплавы; в большинстве
случаев относительная магнитная проницаемость таких веществ нелинейно зависит
от напряженности магнитного поля.
; к таким веществам относятся,
например, ферромагнетики железо, никель, кобальт и их сплавы; в большинстве
случаев относительная магнитная проницаемость таких веществ нелинейно зависит
от напряженности магнитного поля.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.