В схеме «Y-Y без нулевого провода» (Рис. 25.12 б) картина несколько изменяется.
Здесь и в симметричном, и в несимметричном режиме сумма фазных токов по первому закону Кирхгофа равна нулю:
![]() . (25.10)
. (25.10)
Таким образом,
симметричный режим ничем не отличается от симметричного режима в схеме «Y-Y с
нулевым проводом». Можно мысленно соединить нулевые точки нагрузки и генератора
проводом, не имеющим электрического сопротивления. Это значит, что напряжение
между нулевыми точками нагрузки и генератора ![]() в
симметричном режиме равно нулю.
в
симметричном режиме равно нулю.
Но при возникновении
несимметрии напряжение ![]() перестает быть равным
нулю. Это напряжение называют напряжением смещения нейтрали. Как правило,
величина напряжения смещения нейтрали ограничивается требованиями техники
безопасности. Поэтому необходимо принимать специальные меры, предотвращающие слишком
большую несимметрию в схемах «Y-Y без нулевого провода».
перестает быть равным
нулю. Это напряжение называют напряжением смещения нейтрали. Как правило,
величина напряжения смещения нейтрали ограничивается требованиями техники
безопасности. Поэтому необходимо принимать специальные меры, предотвращающие слишком
большую несимметрию в схемах «Y-Y без нулевого провода».
26. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
До сих пор мы рассматривали только линейные электрические цепи, то есть цепи, состоящие из ветвей, сопротивления которых (активные сопротивления и реактивные при неизменной частоте тока) не зависят от токов и напряжений.
В таких цепях сопротивления ветвей – это некоторый параметр, известный заранее. Эта особенность позволяет свести расчет линейной цепи к решению системы уравнений с постоянными коэффициентами (иными словами, системы линейных уравнений).
Совсем другое дело – нелинейные цепи. Нелинейной цепь становится в том случае, если в ней появляется хотя бы один нелинейный элемент.
Вольт-амперная характеристика линейного элемента – это прямая (Рис. 26.1 а), откуда и происходит название «линейный элемент». Тангенс угла наклона прямой – это сопротивление линейного элемента.
Вольт-амперная характеристика нелинейного элемента – это в общем случае произвольная функция (Рис. 26.1 б). В отношении нелинейного элемента можно говорить, что его сопротивление изменяется в зависимости от тока в нем.
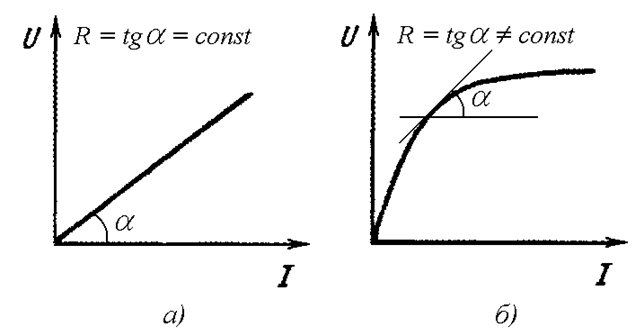
Рис. 26.1
В зависимости от того, активным или реактивным является сопротивление нелинейного элемента, все нелинейные элементы разделяют на резистивные, индуктивные и емкостные. В дальнейшем мы будем иметь в виду лишь резистивные нелинейные элементы. Переход от резистивных нелинейных элементов к индуктивным и емкостным можно осуществить так же, как это сделано в теории линейных цепей синусоидального тока, изложенной в §§16-25.
К нелинейным цепям полностью применимы первый и второй законы Кирхгофа. Поэтому для расчета нелинейных цепей можно пользоваться системой уравнений, составленной по законам Кирхгофа. Правда, эта система уже не будет линейной.
Рассмотрим некоторую цепь, содержащую три нелинейных элемента R1, R2, и R3 (Рис. 26.2). Вольт-амперные характеристики элементов известны – это функции U1(I1), U2(I2), и U3(I3). При необходимости их можно представить в виде I1(U1), I2(U2), и I3(U3). Они описывают связь между токами и напряжениями в ветвях цепи.
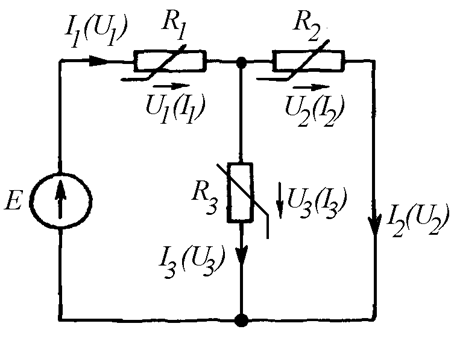
Рис. 26.2
Первый закон Кирхгофа гласит: алгебраическая сумма токов в узле схемы равна нулю. В цепи два узла, поэтому можно составить одно независимое уравнение по первому закону Кирхгофа, например:
![]() . (26.1)
. (26.1)
Второй закон Кирхгофа гласит: в любом замкнутом контуре цепи алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС, включенных в контур. В цепи два независимых контура, поэтому можно составить два независимых уравнения по второму закону Кирхгофа, например:
![]() . (26.2)
. (26.2)
![]() . (26.3)
. (26.3)
Объединяя уравнения (26.1-26.3), получим систему нелинейных алгебраических уравнений:
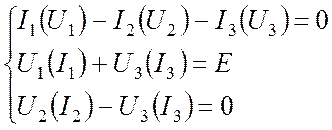 . (26.4)
. (26.4)
Систему (26.4) можно решить численно, графически или любым иным методом, известным в курсе математики. Мы не станем подробно рассматривать методы решения систем нелинейных уравнений. Разберем лишь основные принципы расчета нелинейных цепей на примере двух расчетных методов – графического метода и метода кусочно-линейной аппроксимации.
Графический метод расчета нелинейной цепи
В основе графического метода лежит идея непосредственного приложения законов Кирхгофа к вольт-амперным характеристикам нелинейных элементов. Проиллюстрируем эту идею на примере простейших цепей, состоящих из двух нелинейных элементов.
Пример 26.1
В нелинейной цепи (Рис. 26.3 а) последовательно соединены два нелинейных элемента, вольт-амперные характеристики которых известны (Рис. 26.3 б). Требуется найти ток I* при заданной ЭДС E.
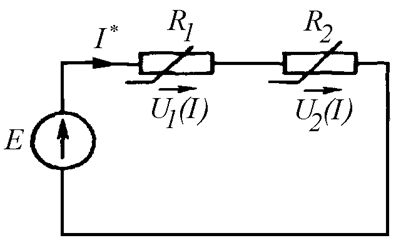
а)
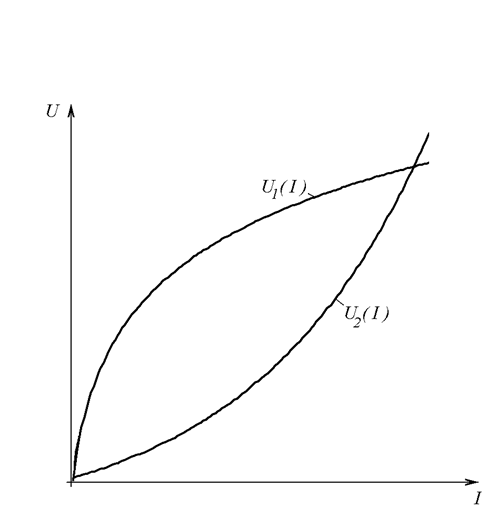
б)
Рис. 26.3
Цепь состоит из одного контура, для которого можно записать уравнение по второму закону Кирхгофа:
![]() . (Пр. 26.1.1)
. (Пр. 26.1.1)
Сумма падений напряжений на нелинейных элементах равна ЭДС E. При этом ток в цепи фиксирован и равен I*.
Заменим два нелинейных элемента одним эквивалентным (Рис. 26.4).
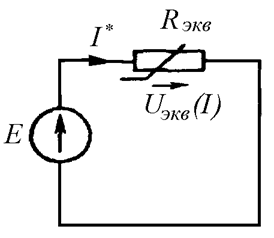
Рис. 26.4
Уравнение по второму закону Кирхгофа для преобразованной цепи имеет вид:
![]() . (Пр. 26.1.2)
. (Пр. 26.1.2)
Сравнивая (Пр. 26.1.1) и (Пр. 26.1.2) видим, что вольт-амперная характеристика эквивалентного нелинейного элемента при изменении тока описывается выражением:
![]() . (Пр. 26.1.3)
. (Пр. 26.1.3)
Строим вольт-амперную характеристику эквивалентного нелинейного элемента, складывая ординаты графиков U1(I) и U2(I) при фиксированных значениях тока (Рис. 26.5 а).
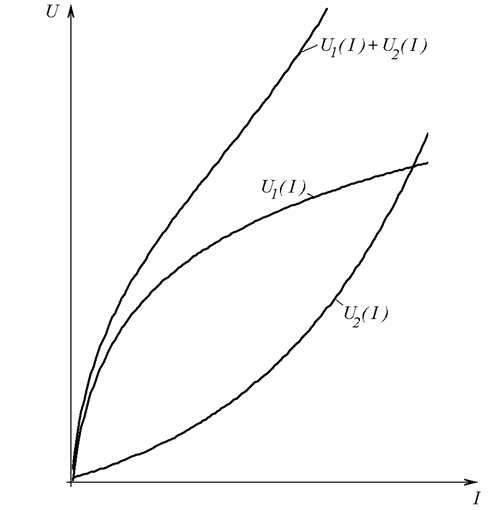
а)
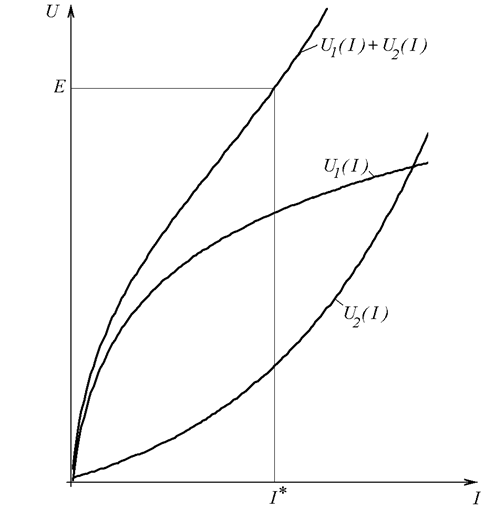
б)
Рис. 26.5
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.