![]() . (11.4)
. (11.4)
Подставим уравнения (11.2-11.4) в (11.1):
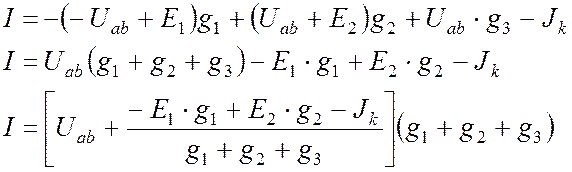 . (11.5)
. (11.5)
Теперь запишем уравнение по закону Ома для эквивалентной ветви (Рис. 11.1 б):
![]() . (11.6)
. (11.6)
Из сравнения (11.6) и (11.5) очевидны соотношения для параметров эквивалентной цепи:
![]() , (11.7)
, (11.7)
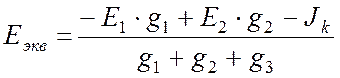 . (11.8)
. (11.8)
Обобщим формулы (11.7) и (11.8) на произвольное количество параллельных ветвей.
Итак, параллельные ветви с источниками энергии можно заменить одной эквивалентной ветвью, содержащей последовательно включенные сопротивление и ЭДС. При этом проводимость эквивалентной ветви равна арифметической сумме проводимостей всех ветвей:
![]() . (11.9)
. (11.9)
Эквивалентная ЭДС равна дроби, в знаменателе которой – сумма проводимостей всех ветвей (как активных, так и пассивных). В числителе – алгебраическая сумма источников тока плюс алгебраическая сумма произведений ЭДС на проводимость своей ветви:
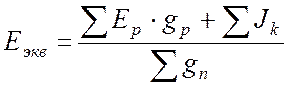 . (11.10)
. (11.10)
где p – число ветвей с ЭДС;
k – число ветвей с источниками тока;
n – число всех ветвей.
В выражении (11.10) с плюсом берутся те ЭДС и источники тока, которые совпадают по направлению с эквивалентной ЭДС, с минусом – противоположные.
Пример 11.1: Найти ток I3 (Рис. 11.2).
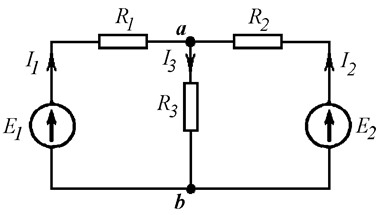
Рис. 11.2
Исходную цепь преобразуем, свернув две активные ветви в одну эквивалентную. При этом ветвь с током I3 преобразованию не подвергнется, а значит, не изменится ток в ней (Рис. 11.3):
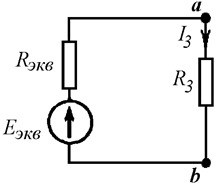
Рис. 11.3
Параметры эквивалентной ветви:
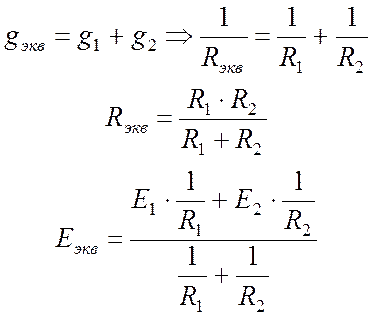 .
.
Очевидно, что в преобразованной схеме (Рис. 11.3) ток I3 легко определяется по закону Ома:
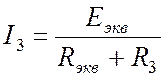 .
.
12. ВЫНЕСЕНИЕ ЭДС И ИСТОЧНИКА ТОКА ИЗ ВЕТВИ
В сложной цепи имеется ветвь с нулевым сопротивлением и идеальной ЭДС (Рис. 12.1).
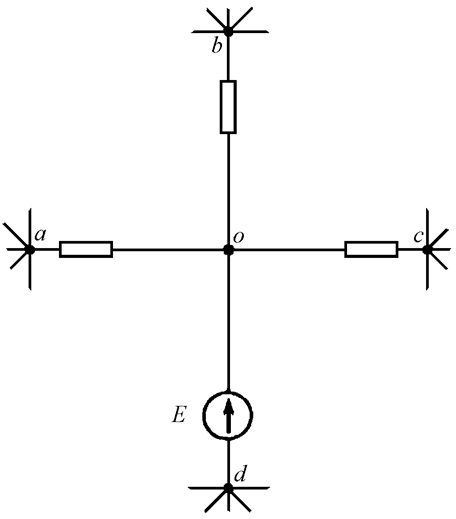
Рис. 12.1
Требуется преобразовать цепь таким образом, чтобы в ней не было ветви с нулевым сопротивлением. Сделать это можно, удалив ЭДС E из ветви. Тогда потенциалы узлов d и o будут равны, эти узлы можно будет объединить и ветвь с нулевым сопротивлением исчезнет.
Идеальная ЭДС E располагается между узлами d и o. Добавим во все ветви, примыкающие к узлу o, такие же ЭДС E, но направленные не к узлу, а от узла (Рис. 12.2). Очевидно, что при этом изменится потенциал узла o, но потенциалы узлов a, b, c и d останутся неизменными.
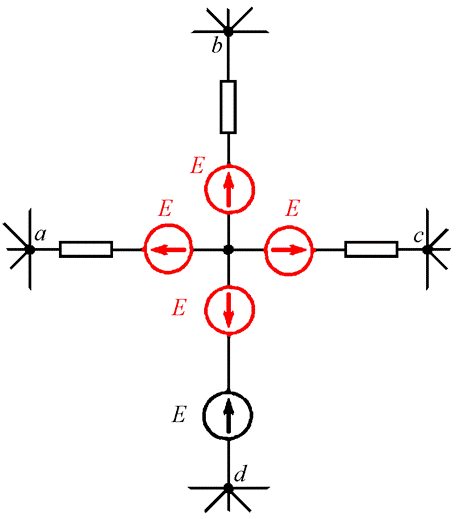
Рис. 12.2
Теперь в ветви с нулевым сопротивлением имеются две равные и противоположно направленные ЭДС. Они компенсируют друг друга, и их можно удалить из ветви (Рис. 12.3).
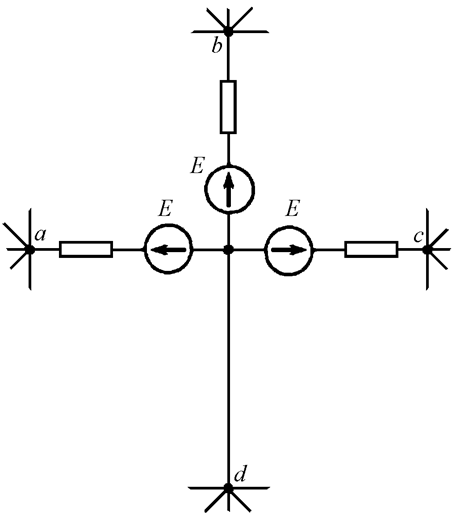
Рис. 12.3
Узлы, соединенные ветвью с нулевым сопротивлением, не содержащей ЭДС, можно объединить. Новый узел будет иметь тот же потенциал, что и у узла d до преобразования. Таким образом, из схемы исключена ветвь с нулевым сопротивлением и узел o (Рис. 12.4).
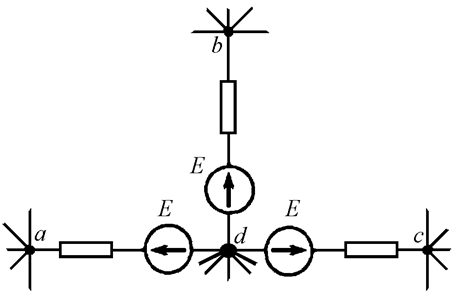
Рис. 12.4
Такая операция называется вынесением ЭДС из ветви за узел. При вынесении ЭДС из ветви за узел вместо исходной ЭДС появляются точно такие же ЭДС в остальных ветвях, примыкающих к узлу, но ориентированные противоположно (если исходная ЭДС была направлена к узлу, то ЭДС в эквивалентной схеме направлены от узла, и наоборот).
Заметим, что вынесение ЭДС из ветви за узел применимо к любым ветвям, а не только к ветвям с нулевым сопротивлением.
Для вынесения источника тока из ветви достаточно включить точно такие же источники тока параллельно другим ветвям, но так, чтобы не изменилось токораспределение в схеме.
Пример 12.1:
Вынести из ветви источник тока (Рис. 12.5).
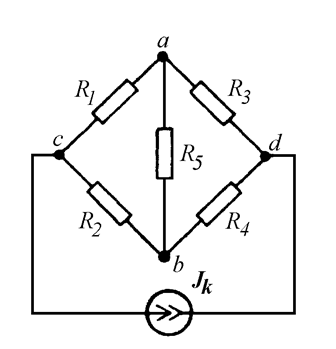
Рис. 12.5
Ток источника Jk вытекает из узла c и втекает в узел d. Значит, и в преобразованной схеме ток Jk должен вытекать из узла c и втекать в узел d (Рис. 12.6).
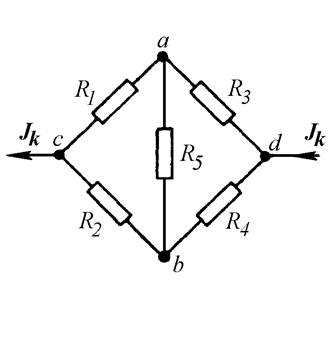
Рис. 12.6
Но если, например, в узел a будет втекать ток Jk и одновременно вытекать ток Jk (Рис. 12.7), распределение токов в схеме не изменится.
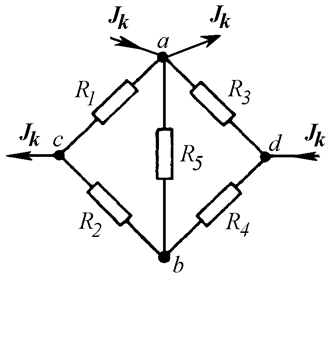
Рис. 12.7
Вышеприведенные рассуждения позволяют нам включить два источника тока параллельно ветвям с резисторами R1 и R3 (Рис. 12.8).
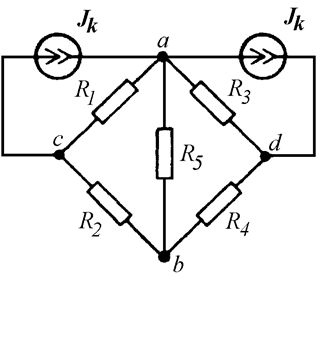
Рис. 12.8
13. МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ
Для расчета токов в электрической цепи достаточно знать потенциалы всех узлов. Тогда с помощью закона Ома можно найти токи.
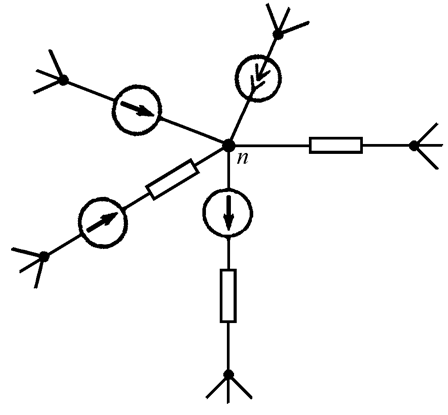
Рис. 13.1
Электрическая цепь – это система ветвей, соединенных друг с другом узлами. Каждая ветвь упирается своими концами в два узла. Справедливо и обратное утверждение: любые два узла цепи соединяются друг с другом ветвью. Это утверждение поможет нам разработать алгоритм определения потенциалов узлов.
Представим задачу в наиболее общем виде. Пусть в узле n соединяется множество ветвей. При этом каждая ветвь на своем противоположном конце также заканчивается узлом (Рис. 13.1).
Все ветви цепи можно условно разбить на три группы.
Первая – ветви, содержащие ЭДС и обладающие конечной проводимостью. Заметим, что к этой же группе можно отнести ветви с конечной проводимостью без ЭДС. Такие ветви будем обозначать индексом i (Рис. 13.2 а).
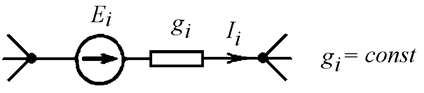
а)
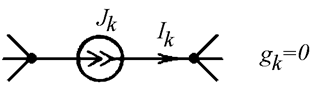
б)
Рис. 13.2
Вторая – ветви, содержащие источники тока. Проводимость этих ветвей равна нулю. Такие ветви будем обозначать индексом k (Рис. 13.2 б).
Третья – ветви с ЭДС и нулевым сопротивлением. Проводимость этих ветвей бесконечно велика. Как было показано выше, такие ветви всегда можно устранить из схемы путем вынесения ЭДС из ветви за узел. Поэтому в дальнейшем будем рассматривать цепь, в которой нет ветвей с ЭДС и нулевым сопротивлением.
Пусть в узле n соединяются i‑ые и k‑ые ветви. Обозначим узлы, противоположные узлу n, индексами i и k (Рис. 13.3). Само собой разумеется, количество i‑ых и k‑ых ветвей может быть каким угодно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.