Основы электротехники и электроники: Курс лекций, страница 5

.

Тогда по закону Ома

.

Но, с другой стороны, по закону Ома

.

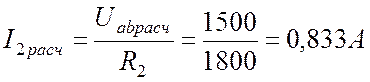По первому закону Кирхгофа

.

Но по закону Ома для участка с ЭДС

.

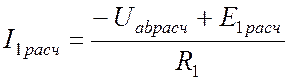Откуда выражаем расчетную ЭДС:

.

Находим коэффициент пересчета:

.

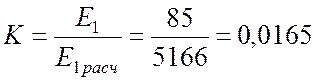Находим реальные токи:

.

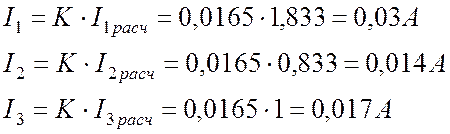Замечание: Так как исходные данные заданы с точностью до двух значащих цифр, окончательные результаты расчетов округляем также до двух значащих цифр, а в промежуточных расчетах оставляем три значащие цифры.

Проверяем расчет при помощи баланса мощности.

Мощность источников

.

Мощность потребителей

.

.

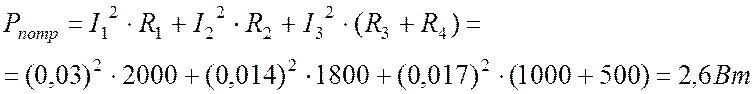8. МЕТОД КОНТУРНЫХ ТОКОВ

При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют реальные токи ветвей.

Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить по второму закону Кирхгофа для независимых контуров. Следовательно, метод контурных токов более экономен, чем метод на основе законов Кирхгофа (в нем меньше уравнений).

Вывод основных расчетных уравнений покажем на примере схемы с двумя независимыми контурами (Рис. 8.1).

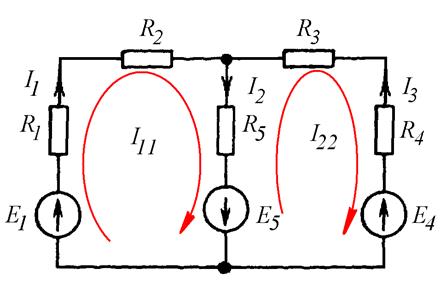
Рис. 8.1

Пусть в левом контуре по часовой стрелке течет контурный ток I₁₁, а в правом (также по часовой стрелке) – контурный ток I₂₂.

Прежде всего, запишем соотношения между контурными и реальными токами. В схеме два контура. Они имеют одну общую ветвь (последовательно соединенные ЭДС E₅ и сопротивление R₅). Следовательно, в этой ветви течет как контурный ток первого контура (I₁₁), так и контурный ток второго контура (I₂₂). Но если контурный ток I₁₁ течет сверху вниз, то контурный ток I₂₂ течет снизу вверх.

Алгебраическая сумма контурных токов будет равна реальному току ветви, то есть току I₂. С учетом направления реального тока имеем:

                                                                        .                   (8.1)

Очевидно, что в остальных ветвях с учетом направления реальных токов:

                                                                              ,                        (8.2)

                                                                            .                       (8.3)

Запишем уравнения по второму закону Кирхгофа для реальных токов:

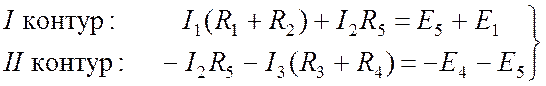                                 .                                                                                 (8.4)

Подставим в (8.4) соотношения (8.1-8.3):

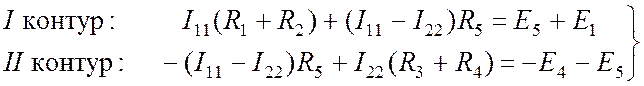                .                                                                                 (8.5)

Перегруппируем слагаемые в (8.5) и получим систему линейных алгебраических уравнений относительно контурных токов:

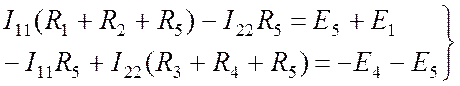                                              .                                                                                 (8.6)

Алгоритм расчета цепи методом контурных токов

1. Выбирается произвольное направление контурных токов в каждом из независимых контуров.
2. По второму закону Кирхгофа составляются уравнения для каждого из независимых контуров с использованием контурных токов. При этом первый закон Кирхгофа выполняется автоматически. В правильно составленной системе уравнений главный определитель симметричен относительно главной диагонали.
3. После расчета полученной системы уравнений для контурных токов определяются реальные токи ветвей как алгебраическая сумма контурных токов. Если по ветви протекает один контурный ток, то реальный ток равен контурному.
4. Правильность расчета можно проверить либо с помощью баланса мощности, либо по второму закону Кирхгофа (но не по первому закону Кирхгофа!).

Пример 8.1:

Найти неизвестные токи методом контурных токов (Рис. 8.2).

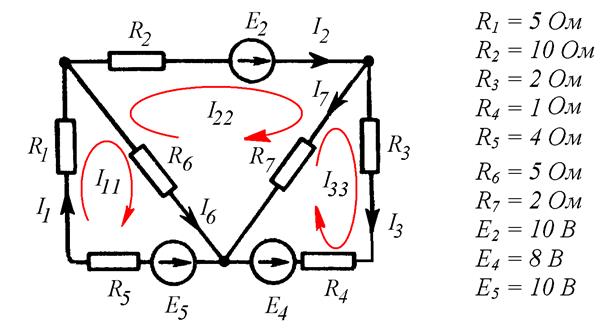
Рис. 8.2

Выбираем независимые контуры по ячейкам схемы. Задаем направления контурных токов. В данном случае направим все контурные токи по часовой стрелке.

Составляем уравнения по второму закону Кирхгофа для контурных токов.

Для I контура. Собственное сопротивление контура состоит из R₁, R₆ и R₅. По ветви с R₆ текут два контурных тока I₁₁ и I₂₂ в противоположных направлениях. Значит, в уравнение по второму закону Кирхгофа для контура I ток I₂₂ войдет с минусом:

                                                       .  (Пр. 8.1.1)

Для II контура. Собственное сопротивление контура состоит из R₂, R₇ и R₆. По ветви с R₆ ток I₁₁ течет противоположно току I₂₂. А ток I₃₃ течет по ветви с R₇ противоположно току I₂₂. Значит, в уравнение по второму закону Кирхгофа для контура II токи I₁₁ и I₃₃ войдут с минусом:

                                                .                                                                            (Пр. 8.1.2)

Для III контура. Собственное сопротивление контура состоит из R₃, R₄ и R₇. По ветви с R₇ течет ток I₂₂ противоположно току I₃₃. Значит, в уравнение по второму закону Кирхгофа для контура III ток I₂₂ войдет с минусом:

                                                      . (Пр. 8.1.3)

Объединяем уравнения (Пр. 8.1.1-Пр. 8.1.3) в систему, следя за тем, чтобы в уравнениях присутствовали все неизвестные токи и располагались они руг под другом. В уравнении (Пр. 8.1.1) нет тока I₃₃. Значит, запишем его, умноженным на ноль. Аналогично поступим с током I₁₁ в уравнении (Пр. 8.1.3):

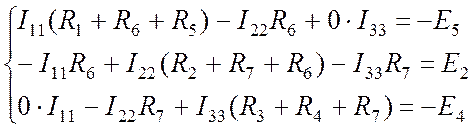                                            .                                                                            (Пр. 8.1.4)

В числах система (Пр. 8.1.4) будет выглядеть так:

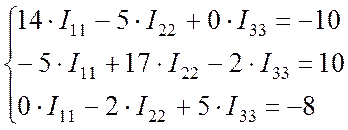                                                        .   (Пр. 8.1.5)

Заметим, что система (Пр. 8.1.5) имеет главный определитель, симметричный относительно главной диагонали.

Систему (Пр. 8.1.5) решим методом Крамера.

Главный определитель системы:

.

.

.

.

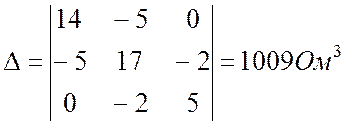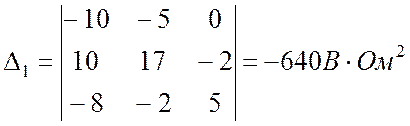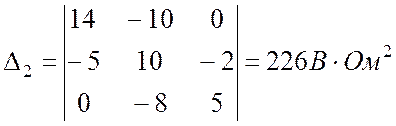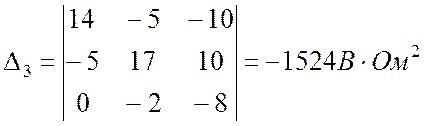Контурные токи:

.

.

.

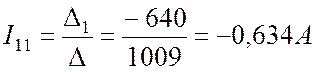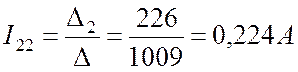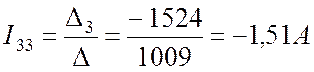Определяем реальные токи (См. Рис. 8.2):

.

.

.

.