Произведение двух сопряженных чисел равно квадрату их модуля, поэтому полная мощность в комплексной форме равна произведению квадрата действующего значения тока (действительного числа) на комплексное сопротивление.
Представив полное сопротивление в (19.20) в алгебраической форме, имеем:
![]() . (19.21)
. (19.21)
Составим баланс мощности в комплексной форме. Полная мощность источников, очевидно, будет описываться выражением:
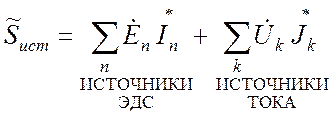 . (19.22)
. (19.22)
Полная мощность потребителей:
![]() . (19.23)
. (19.23)
Баланс мощности в комплексной форме:
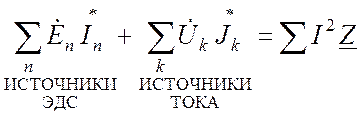 . (19.24)
. (19.24)
В комплексной форме достаточно рассчитать один баланс мощности, а не два баланса активной и реактивной мощности. Баланс мощности (19.24) включает в себя сразу как активную, так и реактивную мощность. При этом автоматически учитываются знаки при реактивных сопротивлениях, а значит, автоматически определяется, индуктивной или емкостной является реактивная мощность.
20. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ RLC
Рассмотрим некоторую цепь с последовательным соединением резистора, индуктивной катушки и конденсатора (Рис. 20.1).
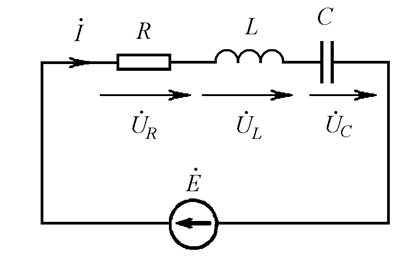
Рис. 20.1
Определим ток в цепи, если ЭДС изменяется по синусоидальному закону:
![]() . (20.1)
. (20.1)
Запишем уравнение по второму закону Кирхгофа для синусоидальных функций:
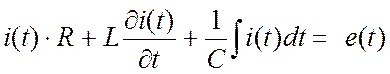 . (20.2)
. (20.2)
Уравнение (20.2) – интегро-дифференциальное, и его решение может быть представлено в виде суммы какого-либо частного решения и решения однородного уравнения. Однородное уравнение – это уравнение с нулевой правой частью. Уравнение превратится в однородное, если ЭДС в цепи будет равна нулю.
Если ЭДС – синусоидальная функция, то частное решение уравнения (20.2) также можно представить в виде синусоидальной функции с той же частотой:
![]() . (20.3)
. (20.3)
Начальная фаза тока в выражении
(20.3) – это пока не известная постоянная. В данном случае ее удобно записать с
минусом, ведь если ![]() – это угол между
напряжением и током на входе, то при нулевой начальной фазе ЭДС начальная фаза
тока – это минус
– это угол между
напряжением и током на входе, то при нулевой начальной фазе ЭДС начальная фаза
тока – это минус ![]() :
:
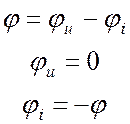 .
.
В
установившемся режиме составляющая тока, обусловленная решением однородного
уравнения (при ![]() ), стремится к нулю,
поэтому далее рассматривать ее не будем.
), стремится к нулю,
поэтому далее рассматривать ее не будем.
Представим ЭДС в виде:
![]()
и преобразуем синус суммы углов, используя формулу:
![]() .
.
![]() . (20.4)
. (20.4)
Подставим (20.3) и (20.4) в (20.2):
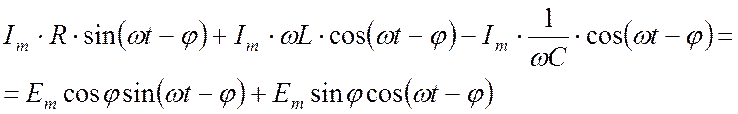 . (20.5)
. (20.5)
Не вызывает
сомнения, что уравнение (20.5) должно быть справедливо для любого момента
времени ![]() , и в частности, при
, и в частности, при ![]() (20.5) принимает вид:
(20.5) принимает вид:
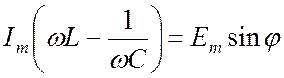 . (20.6)
. (20.6)
При 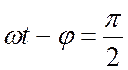 (20.5) принимает вид:
(20.5) принимает вид:
![]() . (20.7)
. (20.7)
Возведем
(20.6) и (20.7) в квадрат и почленно сложим. Так как ![]() , получим:
, получим:
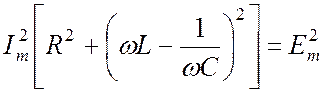 . (20.8)
. (20.8)
Откуда
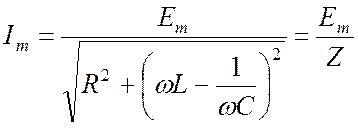 . (20.9)
. (20.9)
Поделив (20.6) на (20.7), получим:
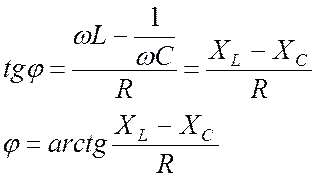 . (20.10)
. (20.10)
Итак, решение интегро-дифференциального уравнения (20.2) имеет вид:
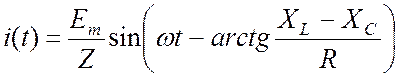 , (20.11)
, (20.11)
где ![]() ,
,
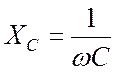 ,
, 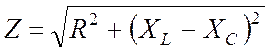 .
.
Сами по себе
реактивные сопротивления ![]() и
и ![]() больше нуля, но эквивалентное реактивное
сопротивление
больше нуля, но эквивалентное реактивное
сопротивление ![]() может быть положительным,
отрицательным и равным нулю.
может быть положительным,
отрицательным и равным нулю.
Проанализируем векторные диаграммы, соответствующие всем трем случаям.
Первый
случай. ![]() ,
, ![]() .
Построение первой векторной диаграммы разберем подробно, ибо здесь чрезвычайно
важна последовательность построения векторов. Выбрав масштабы тока и
напряжения, прежде всего, строим вектор тока, так как ток в цепи один, и все остальные
векторы будем ориентировать относительно вектора тока. Пусть вектор тока направлен
горизонтально слева направо (Рис. 20.2 а).
.
Построение первой векторной диаграммы разберем подробно, ибо здесь чрезвычайно
важна последовательность построения векторов. Выбрав масштабы тока и
напряжения, прежде всего, строим вектор тока, так как ток в цепи один, и все остальные
векторы будем ориентировать относительно вектора тока. Пусть вектор тока направлен
горизонтально слева направо (Рис. 20.2 а).
Далее строим
вектор напряжения на резисторе ![]() , он совпадает по
фазе с током (Рис. 20.2 б).
, он совпадает по
фазе с током (Рис. 20.2 б).
Из конца
вектора ![]() строим вектор
строим вектор ![]() , изображающий падение напряжения на
катушке (Рис. 20.2 в). Этот вектор
направлен вертикально вверх, так как на катушке напряжение опережает ток на
угол
, изображающий падение напряжения на
катушке (Рис. 20.2 в). Этот вектор
направлен вертикально вверх, так как на катушке напряжение опережает ток на
угол ![]() .
.

а)
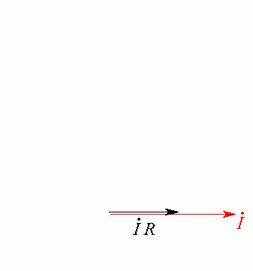
б)
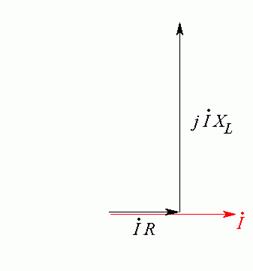
в)
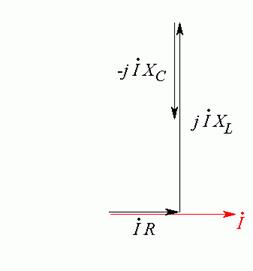
г)
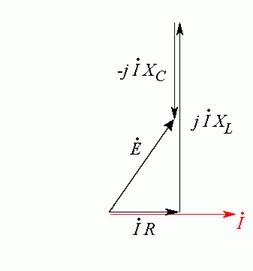
д)
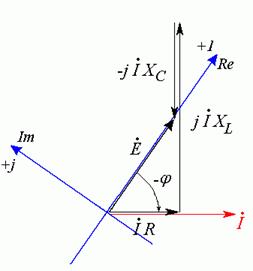
е)
Рис. 20.2
Из конца
вектора ![]() строим вектор
строим вектор ![]() , изображающий падение напряжения на
конденсаторе (Рис. 20.2 г).
Этот вектор направлен вертикально вниз, так как на конденсаторе напряжение
отстает от тока на угол
, изображающий падение напряжения на
конденсаторе (Рис. 20.2 г).
Этот вектор направлен вертикально вниз, так как на конденсаторе напряжение
отстает от тока на угол ![]() .
.
Наконец,
соединяем начало первого вектора с концом последнего. Этот вектор изображает ЭДС
![]() (Рис. 20.2 д).
(Рис. 20.2 д).
Начальная фаза
ЭДС равна нулю, значит, вектор ![]() должен совпадать
с действительной осью на комплексной плоскости. Изображаем действительную и
мнимую оси, а также обозначаем начальную фазу тока (Рис. 20.2 е).
должен совпадать
с действительной осью на комплексной плоскости. Изображаем действительную и
мнимую оси, а также обозначаем начальную фазу тока (Рис. 20.2 е).
В дальнейшем
оси координат нам не понадобятся, поэтому их можно убрать, имея в виду, что
вектор ![]() во всех режимах совпадает с
действительной осью. Заменим на диаграмме угол минус
во всех режимах совпадает с
действительной осью. Заменим на диаграмме угол минус![]() на
угол
на
угол ![]() , как показано на Рис. 20.3.
, как показано на Рис. 20.3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.