Пример 5.1:
Составить
систему уравнений по законам Кирхгофа для определения неизвестных токов ![]() (Рис. 5.1).
(Рис. 5.1).
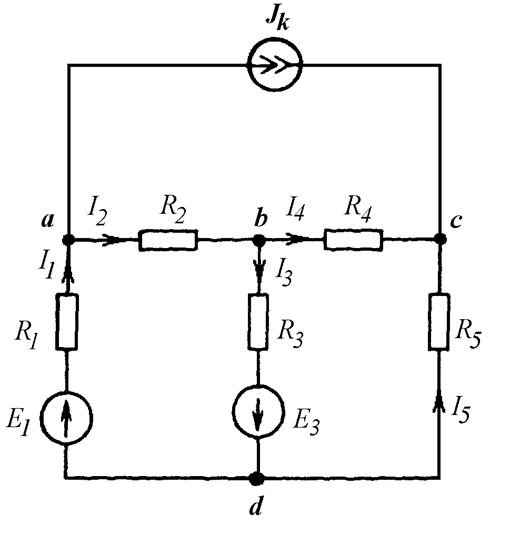
Рис. 5.1
I контур – a-b-d-a
II контур – b-c-d-b
III контур – источник тока-c-b-a
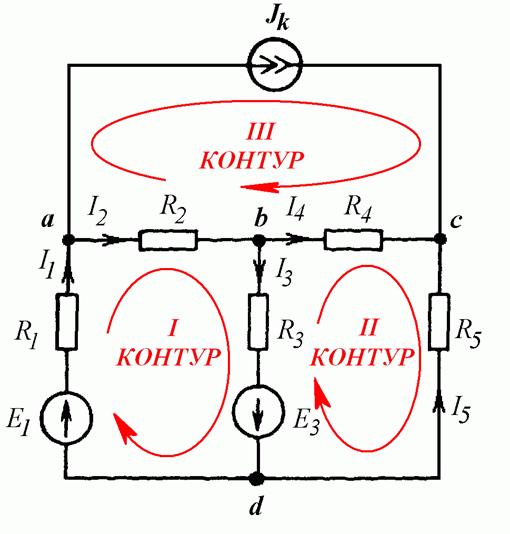
Рис. 5.2
Исключаем из рассмотрения контур с источником тока, оставляем контуры I и II. Выбираем направление обхода по часовой стрелке.
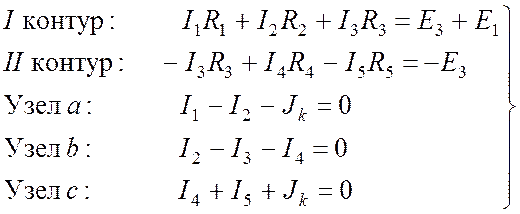
На практике чаще всего пользоваться системой уравнений по законам Кирхгофа затруднительно из-за ее громоздкости. На основе законов Кирхгофа разработаны более экономичные методы расчета токов. А законы Кирхгофа используются для проверки правильности решения и для отыскания напряжений между любыми точками цепи, даже непосредственно не связанными.
6. БАЛАНС МОЩНОСТИ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
В электрической цепи источники создают электрическую энергию, потребители ее расходуют. В соответствии с законом сохранения энергии количество энергии источников должно быть равно количеству энергии потребителей.
В цепи постоянного тока вся энергия, созданная источниками, расходуется в сопротивлениях, преобразуясь в тепло. Это преобразование описывается законом Джоуля-Ленца:
![]() , (6.1)
, (6.1)
где ![]() –
мощность потребителя (то есть энергия, выделяющаяся в потребителе в единицу
–
мощность потребителя (то есть энергия, выделяющаяся в потребителе в единицу
времени);
![]() – ток в ветви с потребителем;
– ток в ветви с потребителем;
![]() – сопротивление потребителя (Рис. 6.1).
– сопротивление потребителя (Рис. 6.1).
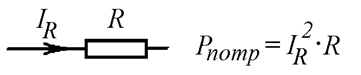
Рис. 6.1
Как видно из выражения (6.1), мощность потребителя – величина всегда положительная и не зависит от направления тока в нем.
Рассмотрим далее источники электрической энергии. Когда источник ЭДС доставляет энергию в электрическую цепь, ток в ветви совпадает по направлению с ЭДС. В этом случае мощность считается положительной (Рис. 6.2 а). Говорят, что ЭДС работает в режиме генератора.
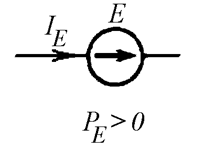
а)
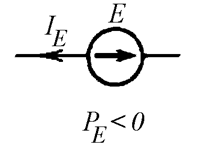
б)
Рис. 6.2
Если же в ветви ток противоположен направлению ЭДС, источник не поставляет энергию в цепь, а потребляет ее. Такое может происходить, например, при заряде аккумулятора. В этом случае мощность считается отрицательной (Рис. 6.2 б). Говорят, что ЭДС работает в режиме приемника.
И в том, и в другом случае мощность ЭДС определяется выражением:
![]() , (6.2)
, (6.2)
где ![]() –
мощность ЭДС;
–
мощность ЭДС;
![]() – ток в ветви с ЭДС.
– ток в ветви с ЭДС.
Если ток совпадает по направлению с ЭДС, он включается в формулу (6.2) с плюсом, если он противоположен ЭДС – с минусом.
Для расчета мощности источника тока используется напряжение на выводах источника. Положительным считается его направление от узла, в который втекает ток источника, к узлу, из которого ток источника вытекает. В этом случае мощность положительна (Рис. 6.3 а).
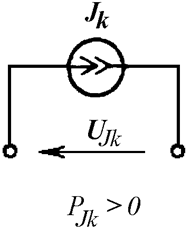
а)
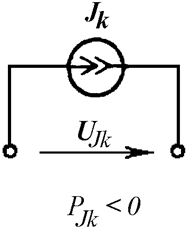
б)
Рис. 6.3
Если напряжение на выводах источника тока направлено от узла, из которого ток вытекает, к узлу, в который ток втекает, мощность источника отрицательна (Рис. 6.3 а). И в том, и в другом случае мощность источника тока определяется выражением:
![]() , (6.3)
, (6.3)
где ![]() –
мощность источника тока;
–
мощность источника тока;
![]() – напряжение на выводах источника
тока.
– напряжение на выводах источника
тока.
Напряжение на выводах источника тока включается в формулу (6.3) с плюсом, когда оно противоположно току источника, и с минусом – когда оно направлено в ту же сторону, что и ток источника.
Для любой электрической цепи справедливо равенство, называемое балансом мощности или энергетическим балансом:
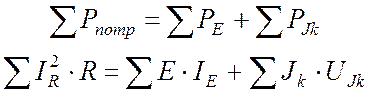 , (6.4)
, (6.4)
Заметим, что в левой части равенства (6.4) сумма арифметическая, а в правой – алгебраическая (с учетом знаков слагаемых).
При расчете мощности источников в балансе (6.4) токи и напряжения на принципиальной схеме надо направлять так, чтобы предполагаемая мощность была положительна.
Баланс мощности (6.4) является независимой проверкой для всех методов расчета электрических цепей.
7. МЕТОД ПРОПОРЦИОНАЛЬНОГО ПЕРЕСЧЕТА
Этот метод расчета применим только к линейным последовательно-параллельным цепям с одним источником энергии и состоит в следующем.
Задается произвольное значение тока в удаленной от источника ветви. После этого находятся расчетные токи во всех ветвях и расчетное напряжение на выводах источника ЭДС (или ток источника тока). Так как расчетное напряжение в общем случае не равно действительному, то токи во всех ветвях следует умножить на коэффициент пересчета:
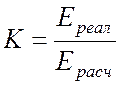 ,
,
где ![]() –
действительное значение ЭДС;
–
действительное значение ЭДС;
![]() – расчетное напряжение на выводах
источника ЭДС.
– расчетное напряжение на выводах
источника ЭДС.
Пример 7.1:
Найти неизвестные токи методом пропорционального пересчета (Рис. 7.1).
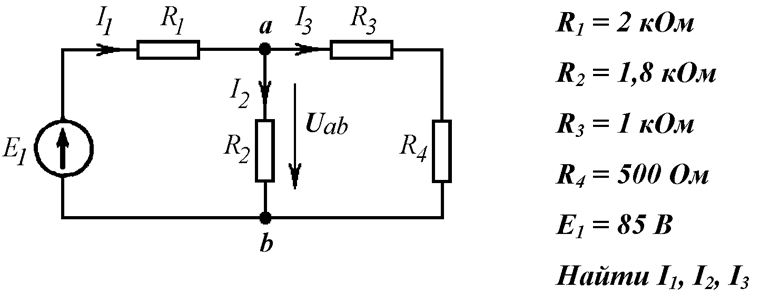
Рис. 7.1
Задаем
расчетное значение тока ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.