Величина, обратная сопротивлению, называется проводимостью (обозначается буквой g, имеет размерность Ом – 1 или См, Сименс).
В линейных цепях сопротивление ветвей постоянно, определяется лишь физическими свойствами материала проводников и не зависит от источников, токов и напряжений в ветвях.
Если источники в цепи создают на своих выводах напряжения и токи, которые не изменяются во времени, цепь называется электрической цепью постоянного тока. В цепи постоянного тока сопротивление индуктивностей равно нулю, сопротивление конденсаторов бесконечно велико.
Далее будут рассмотрены линейные цепи постоянного тока.
2. ИСТОЧНИКИ ЭДС И ИСТОЧНИКИ ТОКА
ЭДС – это максимальное напряжение, которое могут создать сторонние силы на выводах источника при отсутствии в цепи тока. В качестве сторонних сил могут выступать, например, химические реакции в гальванической батарее или момент на валу электрической машины, работающей в режиме генератора.
Для удобства анализа источники электрической энергии представляют либо с помощью идеального источника ЭДС, либо с помощью идеального источника тока. Идеальный источник ЭДС и идеальный источник тока называют также источниками бесконечно большой мощности.
На Рис. 2.1 а показана вольт-амперная характеристика идеального источника ЭДС. Этот источник отличается тем, что напряжение на его выводах равно значению ЭДС независимо от тока нагрузки. На Рис. 2.1 б показана вольт-амперная характеристика идеального источника тока. Он сохраняет постоянство тока вне зависимости от напряжения на своих выводах.
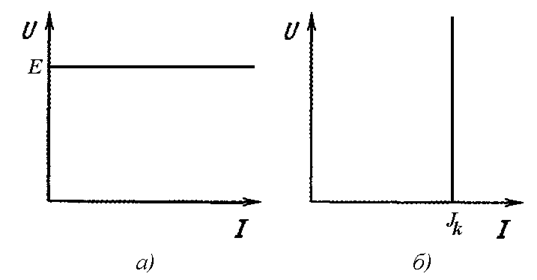
Рис. 2.1
Если к данным вольт-амперным характеристикам применить закон Ома (см. формулу (1.1))
,
можно сделать вывод, что сопротивление идеального источника ЭДС равно нулю, а сопротивление идеального источника тока равно бесконечности.
Реальный источник электрической энергии обладает конечным внутренним сопротивлением, его вольт-амперная характеристика показана на Рис. 2.2 и может быть описана выражением:
(2.1)
где 
–
внутреннее сопротивление источника;
– напряжение холостого хода
источника.
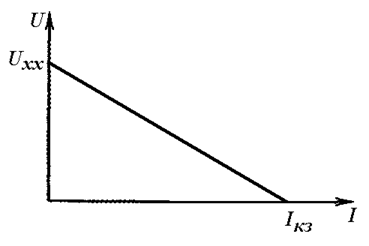
Рис. 2.2
Когда источник
отключен от нагрузки, на его зажимах существует напряжение холостого хода , равное ЭДС источника. Если
соединить накоротко зажимы источника, напряжение на зажимах будет равно нулю, а
ток между зажимами будет равен току короткого замыкания 
.
Сравнивая вольт-амперные характеристики идеальных источников и реального источника, можно заключить, что реальный источник можно смоделировать либо с помощью эквивалентного идеального источника ЭДС и последовательно включенного внутреннего сопротивления, либо с помощью эквивалентного идеального источника тока и параллельно включенного внутреннего сопротивления (Рис. 2.3).
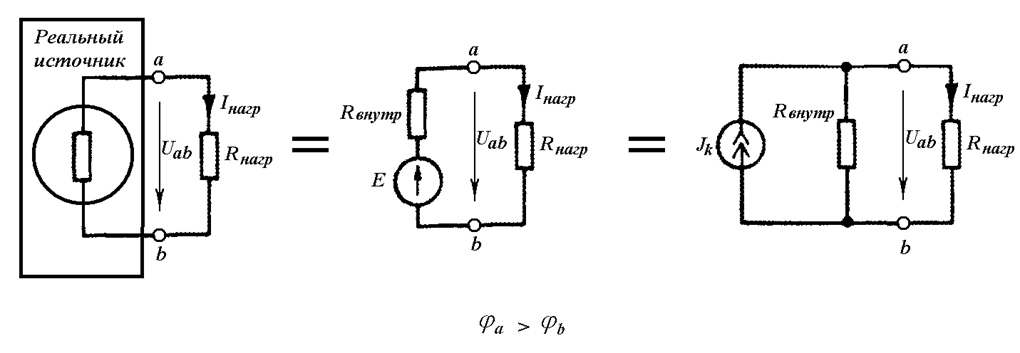
Рис. 2.3
Внутреннее сопротивление реального источника вычисляется как
.
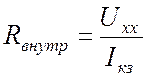ЭДС эквивалентного источника ЭДС равна напряжению холостого хода реального источника.
Ток эквивалентного источника тока равен току короткого замыкания реального источника.
ЭДС эквивалентного источника ЭДС и ток эквивалентного источника тока связаны соотношением:
(2.2)
Это соотношение говорит о том, что любой источник ЭДС с последовательно включенным сопротивлением может быть заменен источником тока с параллельно включенным таким же сопротивлением и наоборот.
Какой из двух эквивалентных замен воспользоваться, совершенно безразлично, и определяется лишь удобством расчета в каждом конкретном случае.
Заметим, что ЭДС идеального источника ЭДС всегда направлена от меньшего потенциала к большему, а ток идеального источника тока всегда направлен в ту же сторону, что и ток реального источника.
3. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ ЦЕПИ
Для упрощения расчетов электрическую цепь можно преобразовывать, уменьшая количество ветвей и узлов. При этом необходимо помнить, что после расчета преобразованной цепи следует выполнить обратное преобразование, чтобы вернуться к исходной цепи.
Любые преобразования цепей должны быть эквивалентными, то есть преобразование какого-либо участка цепи не должно изменять токораспределения в непреобразованной части схемы. А это возможно лишь тогда, когда в процессе преобразования потенциалы узлов в непреобразованной части схемы и токи, подтекающие извне к преобразованному участку, сохраняются неизменными.
Простейшими преобразованиями электрической цепи являются свертки последовательно-параллельных соединений элементов цепи.
При последовательном соединении элементов конец предыдущего соединяется с началом последующего (Рис. 3.1). Главный признак последовательного соединения – один и тот же ток в каждом из элементов.
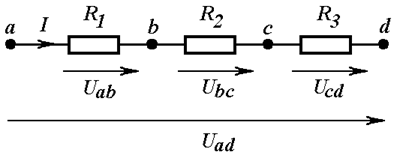
Рис. 3.1
Если к последовательному соединению элементов применить закон Ома (1.1), можно заключить, что напряжения на элементах распределяются прямо пропорционально сопротивлениям, а общее сопротивление последовательного соединения равно сумме сопротивлений элементов:
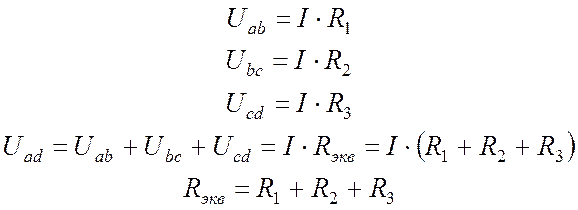(3.1)
Итак, если на участке цепи несколько элементов соединены последовательно, они могут быть заменены одним эквивалентным элементом, сопротивление которого равно сумме сопротивлений отдельных элементов. ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ СОПРОТИВЛЕНИЯ СКЛАДЫВАЮТСЯ!
При параллельном соединении элементов начала всех элементов соединены в один узел, а концы всех элементов соединены в другой узел (Рис. 3.2).
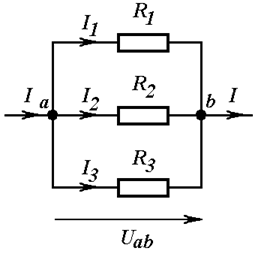
Рис. 3.2
Главный признак параллельного соединения – одно и то же напряжение на каждом из элементов.
Если на участке цепи несколько элементов соединены параллельно, они могут быть заменены одним эквивалентным элементом, проводимость которого равна сумме проводимостей отдельных элементов. ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ СКЛАДЫВАЮТСЯ ПРОВОДИМОСТИ!
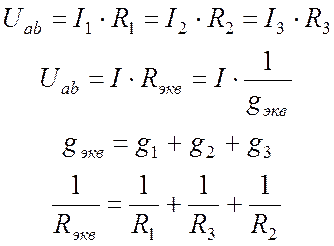(3.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.