Электротехника \ Основы электротехники и электроники

Основы электротехники и электроники: Курс лекций, страница 17

Итак, , . Ток в цепи носит индуктивный характер, так как он отстает от напряжения на входе (вектор ЭДС и вектор напряжения на входе – это один и тот же вектор).

Второй случай. , . Ток в цепи носит емкостной характер, так как он опережает напряжение на входе (Рис. 20.4).

Третий случай. , . Ток в цепи чисто резистивный. Напряжение на входе совпадает с током по фазе и равно напряжению на резисторе (Рис. 20.5). Этот режим называется режимом резонанса напряжений.

Обратить внимание! На векторных диаграммах (Рис. 20.2-Рис. 20.5) для большей наглядности векторы несколько разнесены в пространстве. Если же векторная диаграмма используется как инструмент расчета, этого быть не должно. В частности, в режиме резонанса векторы  и  совпадают, равны по модулю и противоположны по направлению, а векторы  и  – это один и тот же вектор.


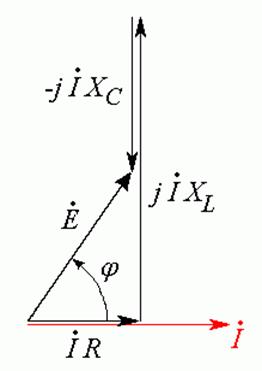
Рис. 20.3

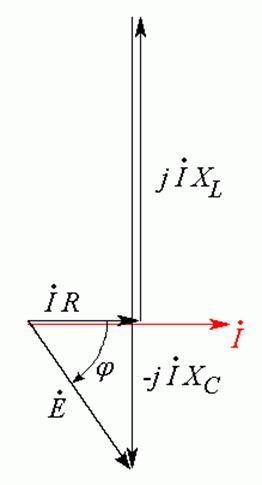
Рис. 20.4

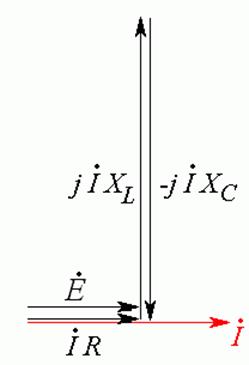
Рис. 20.5



21. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ RLC

Рассмотрим цепь с параллельным соединением резистора, резистора, индуктивной катушки и конденсатора (Рис. 21.1). В данном случае удобнее пользоваться не сопротивлениями ветвей, а их проводимостями, поэтому на схеме резистор обозначен символом проводимости g.

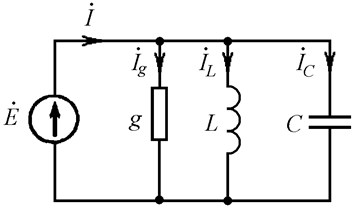
Рис. 21.1

Определим ток на входе цепи, если ЭДС изменяется по синусоидальному закону:

                                                                      .               (21.1)

Запишем уравнение по первому закону Кирхгофа для мгновенных значений токов:

                                                             .      (21.2)

Токи на резисторе, катушке и конденсаторе выразим через ЭДС. Для этого выделим в схеме три независимых контура и запишем для них уравнения по второму закону Кирхгофа:

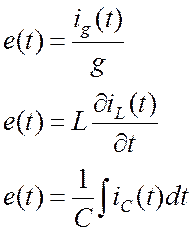                                                                     .             (21.3)

Из (21.3) выразим токи:

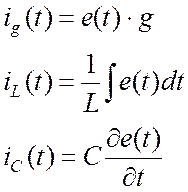                                                                     .              (21.4)

Подставим (21.4) в (21.2) и получим интегро-дифференциальное уравнение относительно тока :

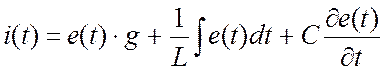                                                    .                                                                                (21.5)

Решение уравнения (21.5) можно получить в виде синусоидальной функции:

                                                                  .           (21.6)


Подставим (21.1) и (21.6) в уравнение (21.5):

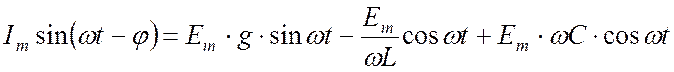           .                                                                                (21.7)

При  выражение (21.7) примет вид:

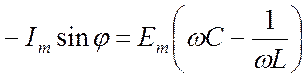                                                           .    (21.8)

При 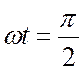 выражение (21.7) примет вид:

                                                                     .             (21.9)

Возведем (21.8) и (21.9) в квадрат и почленно сложим:

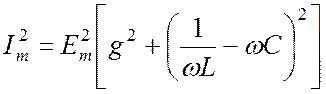                                                         . (21.10)

Откуда:

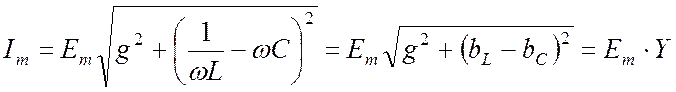           ,                                                                               (21.11)

где 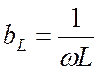      – реактивная проводимость катушки;

             – реактивная проводимость конденсатора;

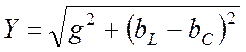             – полная проводимость цепи.

Поделим (21.8) на (21.9):

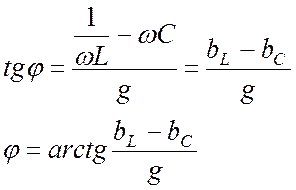                                                            .   (21.12)

Подставим (21.11) и (21.12) в (21.6) и получим решение уравнения (21.5):

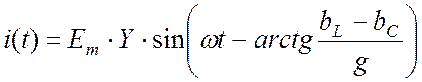                                                 .                                                                               (21.13)

Теперь, как и в предыдущей задаче, рассмотрим векторные диаграммы для различных соотношений  и .

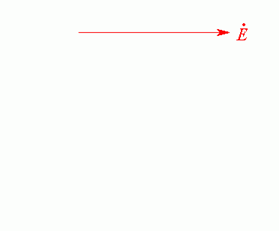
Первый случай. , , . Векторная диаграмма строится так. Так как ко всем элементам схемы приложено одно и то же напряжение, равное ЭДС, сначала строится вектор , относительно которого располагаются все векторы токов. Пусть этот вектор направлен горизонтально слева направо (Рис. 21.2 а).



а)

б)


в)

г)


д)

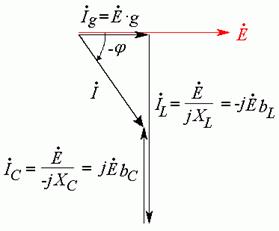
е)

Рис. 21.2

На резисторе ток совпадает по фазе с напряжением. Строим вектор  (Рис. 21.2 б).

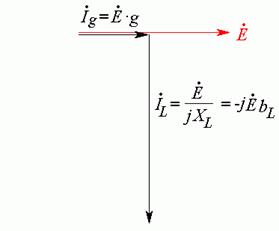
Из конца вектора  строим вектор . Этот вектор направлен вертикально вниз, так как на индуктивности ток отстает от напряжения на угол  (Рис. 21.2 в).

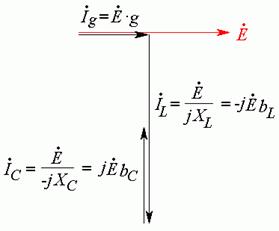
Из конца вектора  строим вектор . Этот вектор направлен вертикально вверх, так как на емкости ток опережает напряжение на угол  (Рис. 21.2 г).

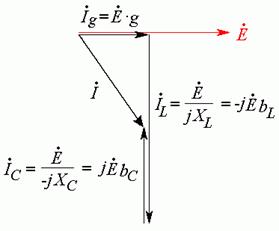
Сумма трех векторов – это вектор тока на входе. Соединяем начало первого вектора с концом последнего и получаем вектор  (Рис. 21.2 д).

Последнее, что осталось сделать – это указать на диаграмме начальную фазу входного тока (Рис. 21.2 е).

Итак, когда , , ток на входе носит индуктивный характер, так как отстает от напряжения на входе (Рис. 21.3).



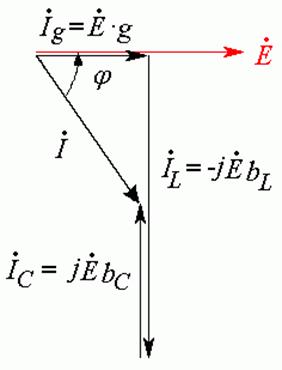
Рис. 21.3

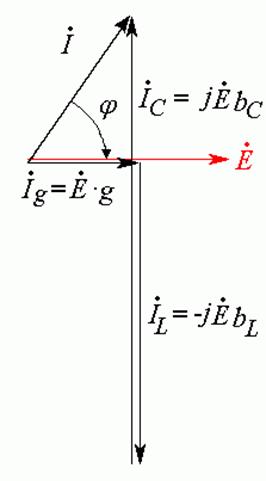
Рис. 21.4

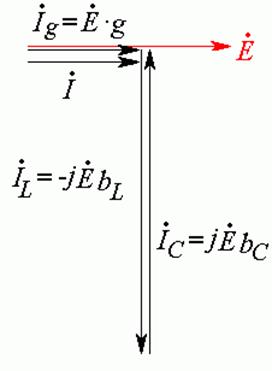
Рис. 21.5


Второй случай. , , . Ток на входе носит емкостной характер, так как опережает напряжение на входе (Рис. 21.4).

Третий случай. , , . Ток в цепи чисто резистивный. Ток на входе совпадает с напряжением по фазе и равен току на резисторе (Рис. 21.5). Этот режим называется режимом резонанса токов.

Обратить внимание! На векторных диаграммах (Рис. 21.2-Рис. 21.5) для большей наглядности векторы несколько разнесены в пространстве, что сказывается на длине векторов. В частности, в режиме резонанса векторы  и  должны совпадать, они должны быть равны по модулю и противоположны по направлению, а векторы  и  – это один и тот же вектор.

22. ПОСЛЕДОВАТЕЛЬНЫЙ РЕЗОНАНС (РЕЗОНАНС НАПРЯЖЕНИЙ)

Резонансом в электрической цепи, содержащей индуктивности и емкости, называется режим, при котором ток на входе цепи совпадает по фазе с входным напряжением. Различают два вида резонанса: резонанс напряжений (в цепи из последовательно соединенных индуктивности и емкости) и резонанс токов (в цепи из параллельно соединенных индуктивности и емкости).

В режиме резонанса цепь ведет себя как активный элемент.

Рассмотрим цепь с последовательным соединением резистора, индуктивной катушки и конденсатора (Рис. 22.1). Такую цепь назовем последовательным колебательным контуром.

Скачать файл